��Ŀ����
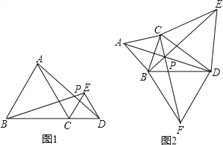
����Ŀ����1����ͼ1����ABC����CDE���ǵȱ������Σ���B��C��D���㹲�ߣ�����AD��BE�ཻ�ڵ�P����֤��BE=AD��
��2����ͼ2������BCD�У���BCD��120�����ֱ���BC��CD��BDΪ������BCD�ⲿ���ȱ�������ABC���ȱ�������CDE�͵ȱ�������BDF������AD��BE��CF���ڵ�P�����н�������ȷ����_________��ֻ����ż��ɣ�
��AD=BE=CF���ڡ�BEC=��ADC���ۡ�DPE=��EPC=��CPA=60����
��3����ͼ2���ڣ�2���������£���֤��PB+PC+PD=BE��
���𰸡���1��BE=AD��2�� �٢ڢ�����ȷ����3��BE=PB+PM+ME=PB+PC+PD��
�������������������1�����ݵȱ������ε����ʵó�BC=AC��CE=CD�� ![]() �����
�����![]() ��֤��
��֤��![]() ���ɣ�
���ɣ�
��2�����BC=AC��CE=CD�� ![]() ��
�� ![]() ��֤
��֤![]() ���Ƴ�
���Ƴ�![]() ��
�� ![]() ��ͬ��
��ͬ��![]() ���Ƴ�BE=CF��
���Ƴ�BE=CF�� ![]() ������
������![]() �Ƴ�
�Ƴ�![]() �����
�����![]() ���������
���������![]() ��ͬ�����
��ͬ�����![]() ��
��
��3����PE�Ͻ�ȡPM=PC������CM�����![]() �����
�����![]() �ǵȱ������Σ��Ƴ�CP=CM��
�ǵȱ������Σ��Ƴ�CP=CM�� ![]() ��֤
��֤![]() ���Ƴ�PD=ME���ɣ�
���Ƴ�PD=ME���ɣ�
���������
��1���ߡ�ABC����CDE���ǵȱ�������
��BC=AC��CE=CD���� ACB=��DCE=60��
���BCE=��ACD
���BCE�ա�ACD��SAS��
��BE=AD
��2���٢ڢ�����ȷ��
��![]() ��
��![]() ���ǵȱ������Σ�
���ǵȱ������Σ�
��![]() ��
�� ![]() ��
�� ![]() ��
��
��![]() ��
��
��![]() ��
��![]() ��
��
![]()
![]()
![]()
![]()
��![]()
��![]() ��
�� ![]() ��
��
�����ȷ��
ͬ��![]()
��BE=CF��
��![]() ��
��
�����ȷ��
��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��
ͬ��![]() ��
��![]()
�����ȷ��
�ʴ�Ϊ���٢ڢ���
��3�� ��PE�Ͻ�ȡPM=PC������CM
�ɣ�1����֪����BCE�ա�ACD��SAS��
���1=��2
��CD��BE���ڵ�G������CGE����PGD��
�ߡ�1=��2����CGE=��PGD
���DPG=��EC G=60��ͬ����CPE=60��
���CPM�ǵȱ�������
��CP=CM����PMC=60����
���CPD=��CME="120" ����
�ߡ�1=��2��
���CPD�ա�CME��AAS����
��PD=ME��
��BE=PB+PM+ME=PB+PC+PD��


 Сѧѧϰ�ð���ϵ�д�
Сѧѧϰ�ð���ϵ�д� Сѧͬ�����������ܾ�ϵ�д�
Сѧͬ�����������ܾ�ϵ�д�
