题目内容
【题目】已知:如图,D是AC上一点,BE∥AC,BE=AD,AE分别交BD、BC于点F、G,且∠1=∠2.
(1)填空:图中与△BEF全等的三角形是______,与△BEF相似的三角形是_____(不再添加任何辅助线);
(2)对(1)中的两个结论选择其中一个给予证明.
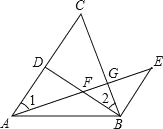
【答案】(1)△BEF≌△DAF;△BEF∽△GBF;(2)证明见解析.
【解析】
(1)结合图形,根据全等三角形的判定即可得解;根据相似三角形的判定,结合图形找出与△BEF能够有两组对应角相等的三角形即可;
(2)根据两直线平行,内错角相等可得∠1=∠E,然后利用“角角边”证明△BEF和△DAF全等;根据∠1=∠2可得∠2=∠E,又∠E为公共角,可以证明△BEF和△GBF相似.
(1)解:△BEF≌△DAF,△BEF∽△GBF;
(2)证明:∵BE∥AC,
∴∠1=∠E,
在△BEF和△DAF中,
∵ ,
,
∴△BEF≌△DAF(AAS);
∵BE∥AC,
∴∠1=∠E,
∵∠1=∠2,
∴∠2=∠E,
又∵∠F为公共角,
∴△BEF∽△GBF.

练习册系列答案
相关题目