Question

已知一次函数y₁=x-1和反比例函数y₂=

2

x

的图象在平面直角坐标系中交于A、B两点，当y₁＜y₂时，x的取值范围是

0＜x＜2或x＜-1

．

Answer 1

分析：将一次函数y₁=x-1和反比例函数y₂=

2

x

组成方程组得到A、B两点坐标，然后画出函数图象，再根据图象求出x的取值范围．

解答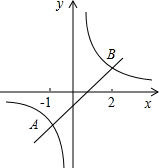：解：将一次函数y₁=x-1和反比例函数y₂=

2

x

组成方程组得，

y=x-1 y= 2 x

，解得

x=-1 y=-2

或

x=2 y=1

．
则A（-1，-2），B（2，1）．
如图：当y₁＜y₂时，x的取值范围是0＜x＜2或x＜-1．
故答案为0＜x＜2或x＜-1．

点评：本题考查了反比例函数与一次函数的交点问题，熟悉函数图象及解析式与函数图象交点的坐标之间的关系是解题的关键．