题目内容
【题目】如图,在平面直角坐标系中,点A和点B的坐标分别为![]() 、
、![]() ,线段CD与AB关于点
,线段CD与AB关于点![]() 中心对称,点A、B的对应点分别为点C、D
中心对称,点A、B的对应点分别为点C、D
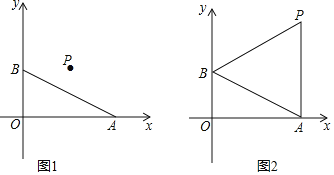
![]() 当
当![]() 时,画出线段CD,并求四边形ABCD的面积;
时,画出线段CD,并求四边形ABCD的面积;
![]() 当
当![]() ______时,四边形ABCD为正方形;
______时,四边形ABCD为正方形;
![]() 当
当![]() 时,连接PA、PB,在OA上有一点M,且
时,连接PA、PB,在OA上有一点M,且![]() ,则点M的坐标为______.
,则点M的坐标为______.
【答案】(1)图形见解析,2;(2)![]() 或
或![]() ;(3)
;(3) ![]() 或
或![]() .
.
【解析】
![]() 线段CD与AB关于点
线段CD与AB关于点![]() 中心对称,得出
中心对称,得出![]() ,
,![]() ,再根据对角线互相平分的四边形是平行四边形,证得四边形ABCD是平行四边形即可求出面积.
,再根据对角线互相平分的四边形是平行四边形,证得四边形ABCD是平行四边形即可求出面积.
![]() 根据四边形ABCD为正方形得出
根据四边形ABCD为正方形得出![]() ,
,![]() ,再根据A、B两点得坐标求得AB的长,从而求出PB的值,构建方程求出m即可.
,再根据A、B两点得坐标求得AB的长,从而求出PB的值,构建方程求出m即可.
![]() 如图3中,以PB为斜边作等腰直角三角形
如图3中,以PB为斜边作等腰直角三角形![]() ,以G为圆心,GB为半径作
,以G为圆心,GB为半径作![]() ,
,![]() 交x轴于M,
交x轴于M,![]() ,则
,则![]() 构造全等三角形求出点G坐标,再求出MH的值即可解决问题.
构造全等三角形求出点G坐标,再求出MH的值即可解决问题.
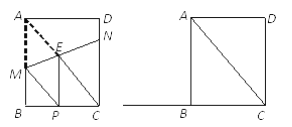
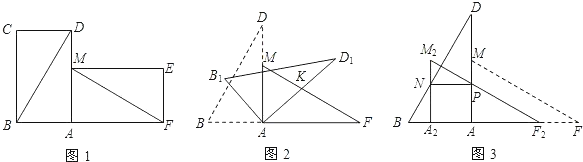
解:![]() 如图1中,
如图1中,
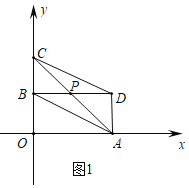
线段CD与AB关于点![]() 中心对称,
中心对称,
![]() ,
,![]() ,
,
![]() 四边形ABCD是平行四边形,
四边形ABCD是平行四边形,
![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() .
.
![]() 如图2中,
如图2中,
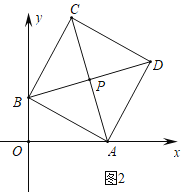
![]() 四边形ABCD是正方形,
四边形ABCD是正方形,
![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
解得![]() 或
或![]() ,
,
故答案为![]() 或
或![]() .
.
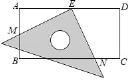
![]() 如图3中,以PB为斜边作等腰直角三角形
如图3中,以PB为斜边作等腰直角三角形![]() ,以G为圆心,GB为半径作
,以G为圆心,GB为半径作![]() ,
,![]() 交x轴于M,
交x轴于M,![]() ,则
,则![]() .
.
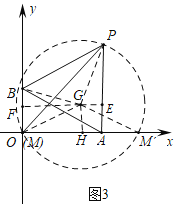
![]() ,
,![]() ,
,
![]() ,
,![]() ,设
,设![]() ,
,
作![]() 交PA于E,作
交PA于E,作![]() 于H,连接GM,
于H,连接GM,![]() .则
.则![]() ≌
≌![]() ,
,
![]() ,
,![]() ,
,
可得![]() ,
,
解得![]() ,
,
![]() ,
,
在![]() 中,
中,![]() ,
,
![]() ,
,![]() .
.
故答案为![]() 或
或![]() .
.

练习册系列答案
相关题目