题目内容
【题目】如图,已知抛物线y=x2+bx+c与y轴交于点C,与x轴交于点A、B,且AB=2,抛物线的对称轴为直线x=2;
(1)求抛物线的函数表达式;
(2)如果抛物线的对称轴上存在一点P,使得△APC周长的最小,求此时P点坐标
及△APC周长;
(3)设D为抛物线上一点,E为对称轴上一点,若以点A、B、D、E为顶点的四边形是平行四边形,求点D的坐标.(直接写出结果)
【答案】(1)y=x2﹣4x+3(2)3![]() +
+![]() (3)(2,﹣1)、(0,3)、(4,3)
(3)(2,﹣1)、(0,3)、(4,3)
【解析】
试题分析:(1)由AB=2,抛物线的对称轴为x=2,得知抛物线与x轴交点为(1,0)、(3,0),即1、3为方程x2+bx+c=0的两个根,结合跟与系数的关系可求得b、c;
(2)由抛物线的对称性,可得出PA+PC最短时,P点为线段BC与对称轴的交点,由此可得出结论;
(3)平行四边形分两种情况,一种AB为对角线,由平行四边形对角线的性质可求出D点坐标;另一种,AB为一条边,根据对比相等,亦能求出D点的坐标.
试题解析:(1)∵AB=2,对称轴为直线x=2,
∴点A的坐标为(1,0),点B的坐标为(3,0),
∵抛物线y=x2+bx+c与x轴交于点A,B,
∴1,3是方程x2+bx+c=0的两个根,
由根与系数的关系,得1+3=﹣b,1×3=c,
∴b=﹣4,c=3,
∴抛物线的函数表达式为y=x2﹣4x+3.
(2)连接AC,BC,BC交对称轴于点P,连接PA,如图1,

由(1)知抛物线的函数表达式为y=x2﹣4x+3,点A,B的坐标分别为(1,0),(3,0),
∴点C的坐标为(0,3),
∴BC=![]() =3
=3![]() ,AC=
,AC=![]() =
=![]() .
.
∵点A,B关于对称轴直线x=2对称,
∴PA=PB,
∴PA+PC=PB+PC,此时,PB+PC=BC,
∴当点P在对称轴上运动时,PA+PC的最小值等于BC,
∴△APC周长的最小值=AC+AP+PC=BC+AC=3![]() +
+![]() .
.
(3)以点A、B、D、E为顶点的四边形是平行四边形分两种情况,
①线段AB为对角线,如图2,
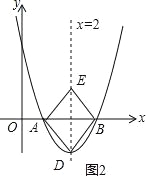
∵平行四边对角线互相平分,
∴DE在对称轴上,此时D点为抛物线的顶点,
将x=2代入y=x2﹣4x+3中,得y=﹣1,
即点D坐标为(2,﹣1).
②线段AB为边,如图3,

∵四边形ABDE为平行四边形,
∴ED=AB=2,
设点E坐标为(2,m),则点D坐标为(4,m)或(0,m),
∵点D在抛物线上,
将x=0和x=4分别代入y=x2﹣4x+3中,解得m均为3,
故点D的坐标为(4,3)或(0,3).
综合①②得点D的坐标可以为:(2,﹣1)、(0,3)、(4,3).
