题目内容
【题目】如图,在某建筑物AC上挂着宣传条幅BC,小明站在点F处,看条幅顶端B,测得仰角为30°,再往条幅方向前行40米到达点E处,看到条幅顶端B,测得仰角为60°.
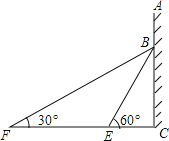
(1)求宣传条幅BC的长(小明的身高不计,结果保留根号);
(2)若小明从点F到点E用了80秒钟,按照这个速度,小明从点F到点C所用的时间为多少秒?
【答案】(1)建筑物BC的长为34.6m.(2)小明从点F到点C所用的时间为120秒.
【解析】
试题分析:(1)设CE=x,根据勾股定理及直角三角形的性质表示出BC、BE长,利用等角对等边易得BE=FE,那么就求得了CE长,进而求得BC长.
(2)根据(1)的结果可求得CF=60,根据已知求得小明的速度,然后根据速度、时间、路程的关系即可求得.
解:设CE=x
在Rt△BCE中,∠BCE=90°,∠BEC=60°
∴∠EBC=30°.
由勾股定理得:BE=2x,BC=![]() x,
x,
∵∠BEC=60°,∠F=30°
∴∠FBE=30°,
∴∠FBE=30°,
∴∠FBE=∠F,
∴BE=EF=2x,
∴EF=40,
∴2x=40,
∴x=20,
∴BC=20![]() .
.
答:建筑物BC的长为34.6m.
(2)∵CE=20,EF=40,
∴CF=60,
小明的速度为40÷80=0.5(米/秒),
小明从点F到点C所用的时间为60÷0.5=120秒
答:小明从点F到点C所用的时间为120秒.

练习册系列答案
相关题目