题目内容
【题目】如图,正方形ABCD中,AB=6,点E在边CD上,且DE=2.将△ADE沿AE对折得到△AFE,延长EF交边BC于点G,则BG=___________.
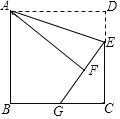
【答案】4
【解析】如图,连接AG,根据折叠的性质以及正方形的性质可证得Rt△ABG≌Rt△AFG,从而可得BG=FG,在Rt△CEG中,利用勾股定理即可得答案.
如图,连接AG,
∵四边形ABCD是正方形,∴AD=BC=CD=AB=6,∠B=∠C=∠D=90°,
由折叠可知AF=AD,EF=DE=2,∠AFE=∠D=90°,
∴∠AFG=90°,
∴AB =AF,
又∵AG=AG,∠B=∠AFG=90°,
∴Rt△ABG≌Rt△AFG(HL),
∴BG=FG,
在Rt△CEG中,EG2=CG2+EC2,
CG=BC-BG=6-BG,CE=CD-DE=6-2=4,EG=EF+FG=BG+2,
∴(BG+2)2=(6-BG)2+42,
∴BG=3,
故答案为:3.

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案
相关题目