题目内容
如图，把矩形纸片ABCD沿着EF折叠，使点B落在边AD上的点D处．点A落在点A′．（1）试说明DE=BF；
（2）若AB=6，AD=8，求AE的长．
分析：（1）利用翻折变换和矩形的性质得出∠2=∠3，∠1=∠3，即可求出DE=BF；
（2）利用勾股定理得出A′D 2+A′E 2=DE 2，进而求出AE的长即可．
（2）利用勾股定理得出A′D 2+A′E 2=DE 2，进而求出AE的长即可．
解答：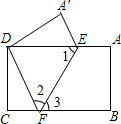
（1）证明：∵把矩形纸片ABCD沿着EF折叠，使点B落在边AD上的点D处，点A落在点A′．
∴∠2=∠3，∠1=∠3，
∴∠1=∠2，
∴DE=DF，
∵DF=BF，
∴DE=BF；
（2）解：设AE=x，则A′E=x，DE=8-x，
∵A′D 2+A′E 2=DE 2，
∴6 2+x 2=（8-x） 2，
解得：x=
，
即AE的长为
．
（1）证明：∵把矩形纸片ABCD沿着EF折叠，使点B落在边AD上的点D处，点A落在点A′．∴∠2=∠3，∠1=∠3，
∴∠1=∠2，
∴DE=DF，
∵DF=BF，
∴DE=BF；
（2）解：设AE=x，则A′E=x，DE=8-x，
∵A′D 2+A′E 2=DE 2，
∴6 2+x 2=（8-x） 2，
解得：x=
| 7 |
| 4 |
即AE的长为
| 7 |
| 4 |
点评：此题主要考查了翻折变换的性质以及勾股定理等知识，利用翻折变换前后对应边对应角相等是解题关键．
练习册系列答案
学练快车道口算心算速算天天练系列答案
相关题目
22、如图，把矩形纸片ABCD沿EF折叠，使点B落在边AD上的点B′处，点A落在点A′处；
（2009•自贡）如图，把矩形纸片ABCD沿EF折叠，使点B落在AD边上的点B′处，点A落在A′处．
如图，把矩形纸片ABCD沿EF折叠后，使得点D与点B重合，点C落在点C′的位置上．
10、如图，把矩形纸片ABCD沿EF折叠，使点B落在AD边上的点B′处，点A落在点A′处．设AE=a，AB=b，BF=c，下列结论：