题目内容
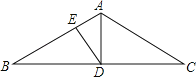
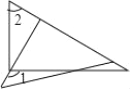
【题目】如图所示，在△ABC中，∠BAC=90°，AD⊥BC于D，BF平分∠ABC，交AD于E，若AE=13，求AF的长度．
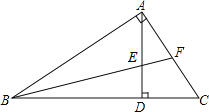
【答案】AF=13
【解析】
试题分析：由∠BAC=90°，于是得到∠ABF+∠AFB=90°，根据垂直的定义得到∠ADB=90°，于是得到∠EBD+∠BED=90°，根据角平分线的定义得到∠ABF=∠EBD，等量代换得到∠AFB=∠BED，∠AEF=∠AFB，根据等腰三角形的判定定理即可得到结论．
解：∵∠BAC=90°，
∴∠ABF+∠AFB=90°，
又∵AD⊥BC，
∴∠ADB=90°，
∴∠EBD+∠BED=90°，
又∵BF平分∠ABC，
∴∠ABF=∠EBD，
∴∠AFB=∠BED，
又∵∠AEF=∠BED，
∴∠AEF=∠AFB，
∴AE=AF，
∵AE=13，
∴AF=13．
练习册系列答案
相关题目
【题目】某酒店有三人间、双人间客房若干，各种房型每天的收费标准如下：
普通（元/间） | 豪华（元/间） | |
三人间 | 160 | 400 |
双人间 | 140 | 300 |
一个50人的旅游团到该酒店入住，选择了一些三人普通间和双人豪华间入住，且恰好住满．已知该旅游团当日住宿费用共计4020元，问该旅游团入住的三人普通间和双人豪华间各为几间？
