Question

在△ABC中，已知I为内心，O为外心，AB=8，BC=6，CA=4．求证：OI⊥CI．

Answer 1

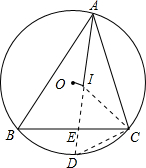证明：∵I是内心，
∴，=．
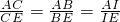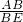又∵AB=8，BC=6，CA=4
∴AC+AB=2BC，
∴AB=2BE．由△ABE∽△ADC知AD=2DC．
又∵DC=DI（内心性质），
∴AD=2DI．
而O是外心，
∴OI⊥AI．
分析：因I是内心，故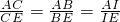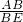，=．又因AB=8，BC=6，CA=4，所以AC+BC=2BC，故AB=2BE．由△ABE∽△ADC知AD=2DC．又DC=DI（内心性质），故AD=2DI．从而即可证明．
点评：本题考查了相似三角形的性质与判定及三角形内切圆与内心，难度适中，关键是掌握外心与内心的性质．