题目内容
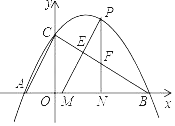
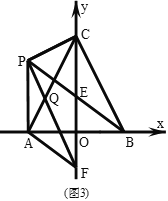
【题目】如图,![]() 为
为![]() 的角平分线,
的角平分线,![]() ,
,![]() 在
在![]() 延长线上,且
延长线上,且![]() ,若
,若![]() ,则
,则![]() 的长为______.
的长为______.
【答案】![]()
【解析】
过点D作DF//AB,交AC于点F,根据已知条件易证AF=BD=FD,再证明△ABD△EFD,得到AB=EF=6,即可得CF=4;由DF//AB,可得△CDF ΔCBA,根据相似三角形的性质可得![]() ,即可得
,即可得![]() ,由此求得BD即可.
,由此求得BD即可.
过点D作DF//AB,交AC于点F,
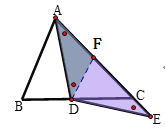
∴∠DFC=∠BAC,∠ABC=∠FDC,
∵AC=BC,
∴∠BAC=∠ABC,
∴∠DFC =∠FDC,
∴CD=CF,
∴BD=AF;
∵AD为△ABC的角平分线,
∴∠BAD=∠DAC,
∵AD=DE,
∴∠DAE=∠DEA,
∴∠BAD=∠DEF,
在△ABD和△EFD中,
∠BAD=∠DEF,∠ABD=∠EFD,AD=DE,
∴△ABD△EFD,
∴AB=EF=6,
∴CF=4,
∵DF//AB,
∴∠ADF=∠BAD,
∵∠BAD=∠DAC,
∴∠ADF=∠DAF,
∴AF=DF,
∴AF=DF=BD,
∵DF//AB,
∴△CDF ΔCBA,
∴![]() ,
,
即![]() ,
,
∴![]() ,
,
解得BD=![]() 或BD=
或BD=![]() (舍去),
(舍去),
∴BD=![]() .
.
故答案为:![]() .
.

练习册系列答案
相关题目
【题目】高速公路某收费站出城方向有编号为![]() 的五个小客车收费出口,假定各收费出口每20分钟通过小客车的数量分别都是不变的.同时开放其中的某两个收费出口,这两个出口20分钟一共通过的小客车数量记录如下:
的五个小客车收费出口,假定各收费出口每20分钟通过小客车的数量分别都是不变的.同时开放其中的某两个收费出口,这两个出口20分钟一共通过的小客车数量记录如下:
收费出口编号 |
|
|
|
|
|
通过小客车数量(辆) | 260 | 330 | 300 | 360 | 240 |
在![]() 五个收费出口中,每20分钟通过小客车数量最多的一个出口的编号是___________.
五个收费出口中,每20分钟通过小客车数量最多的一个出口的编号是___________.