题目内容
将一把三角尺放在边长为1的正方形ABCD上,并使它的直角顶点P在对角线AC上滑动,直角的一边始终经过点B,另一边与射线DC相交于点Q.设A、P两点间的距离为x.(1)当点Q在边CD上时,请你测量线段PQ与线段PB的长度(至少两次),将你测量的实际结果填入下表,由此猜想线段PQ与线段PB之间有怎样的大小关系并证明你得到的结论;
| 线段PQ的长度 | 线段PB的长度 | |
| 第一次 | ||
| 第二次 |
(3)当点Q在边DC的延长线上时,设线段CQ的长度为y,求y与x之间的函数解析式,并写出x的取值范围;
(4)当点P在线段AC上滑动时,△PCQ的面积s能否等于
3
| ||
| 8 |
| 1 |
| 16 |
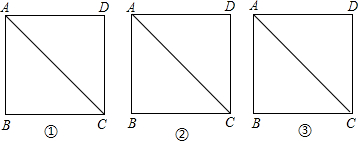
分析:(1)测量略.PB=PQ
可通过构建全等三角形来证PB=PQ,过点P作PF⊥BC于点F,PE⊥CD于点E,由于△PEC是等腰直角三角形,因此PE=EC,可得出四边形PECF是正方形,由此可得出PE=PF,根据同角的余角相等可得出∠FPB=∠QPE,这两个三角形中又有一组直角,因此构成了全等三角形判定条件中ASA的条件.根据全等三角形即可得出PB=PQ.
(2)可先用x表示出PC,然后在直角三角形PFC中求出FC的长,即可求出BF的长,也就求出了CE,QE的长,然后根据CQ=CE-QE即可得出y,x的函数关系式.
(3)当Q在CD延长线上时,CQ=EQ-EC,解法同(2).
(4)由于△PCQ面积最大时,P与A重合,Q与D重合,此时面积为
<
,因此无论什么时候面积都不可能是
.
当面积为
时,可根据(2)(3)两种情况进行分类讨论,通过得出不同的函数关系式,进而根据函数的性质得出符合条件的x的值.
可通过构建全等三角形来证PB=PQ,过点P作PF⊥BC于点F,PE⊥CD于点E,由于△PEC是等腰直角三角形,因此PE=EC,可得出四边形PECF是正方形,由此可得出PE=PF,根据同角的余角相等可得出∠FPB=∠QPE,这两个三角形中又有一组直角,因此构成了全等三角形判定条件中ASA的条件.根据全等三角形即可得出PB=PQ.
(2)可先用x表示出PC,然后在直角三角形PFC中求出FC的长,即可求出BF的长,也就求出了CE,QE的长,然后根据CQ=CE-QE即可得出y,x的函数关系式.
(3)当Q在CD延长线上时,CQ=EQ-EC,解法同(2).
(4)由于△PCQ面积最大时,P与A重合,Q与D重合,此时面积为
| 1 |
| 2 |
3
| ||
| 8 |
3
| ||
| 8 |
当面积为
| 1 |
| 16 |
解答: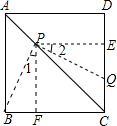 解:(1)(说明:表略,两线段长度基本相等即可)经测量,得PB=PQ
解:(1)(说明:表略,两线段长度基本相等即可)经测量,得PB=PQ
证明:如图,过点P作PF⊥BC于点F,PE⊥CD于点E,
∵∠PCE=45°,∠PEQ=90°,
∴PE=EC.
∴四边形PFCE是正方形.
∴PE=PF.
∵∠BPF=∠QPE=90°-∠FPQ,∠BFP=∠PEQ=90°,
∴△BPF≌△QPE.
∴BP=PQ;
(2)∵AP=x,CQ=y,
∵AB=BC=1,
∴AC=
,
∵PFCE是正方形,
∴PC=
-x,
∴CE=1-
x,
∴BF=1-FC=1-(1-
x),
=
x,
∴EQ=
x,
∴y=CQ=(1-
x)-
x=1-
x,
∴y=1-
x(0≤x≤
);
(3)由(2)易证:当点Q在边DC的延长线上时,
∵PC=
-x,利用勾股定理得出:
∴EC=1-
x,
EQ=BF=MP=
x,
CQ=EQ-EC=
x-1
Y=
x-1(
≤x≤
);
(4)当点P在线段AC上滑动时,△PCQ的最大面积为
∴△PCQ的面积不可能是
当0≤x≤
时,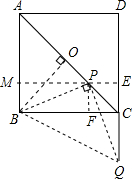
S=
-
x+
x2=
解得x1=
(舍去),x2=
∴此时x=
10分
当
≤x≤
时
S△PCQ=
CQ•PE=-
+
-
x2=
解得x3=x4=
.
综上所述,当P在线段AC上滑动时,△PCQ的面积不可能为
,可能为
.
此时x的值为
和
.
 解:(1)(说明:表略,两线段长度基本相等即可)经测量,得PB=PQ
解:(1)(说明:表略,两线段长度基本相等即可)经测量,得PB=PQ证明:如图,过点P作PF⊥BC于点F,PE⊥CD于点E,
∵∠PCE=45°,∠PEQ=90°,
∴PE=EC.
∴四边形PFCE是正方形.
∴PE=PF.
∵∠BPF=∠QPE=90°-∠FPQ,∠BFP=∠PEQ=90°,
∴△BPF≌△QPE.
∴BP=PQ;
(2)∵AP=x,CQ=y,
∵AB=BC=1,
∴AC=
| 2 |
∵PFCE是正方形,
∴PC=
| 2 |
∴CE=1-
| ||
| 2 |
∴BF=1-FC=1-(1-
| ||
| 2 |
=
| ||
| 2 |
∴EQ=
| ||
| 2 |
∴y=CQ=(1-
| ||
| 2 |
| ||
| 2 |
| 2 |
∴y=1-
| 2 |
| ||
| 2 |
(3)由(2)易证:当点Q在边DC的延长线上时,
∵PC=
| 2 |
∴EC=1-
| ||
| 2 |
EQ=BF=MP=
| ||
| 2 |
CQ=EQ-EC=
| 2 |
Y=
| 2 |
| ||
| 2 |
| 2 |
(4)当点P在线段AC上滑动时,△PCQ的最大面积为
| 1 |
| 2 |
∴△PCQ的面积不可能是
3
| ||
| 8 |
当0≤x≤
| ||
| 2 |

S=
| 1 |
| 2 |
3
| ||
| 4 |
| 1 |
| 2 |
| 1 |
| 16 |
解得x1=
3
| ||
| 4 |
3
| ||
| 4 |
∴此时x=
3
| ||
| 4 |
当
| ||
| 2 |
| 2 |
S△PCQ=
| 1 |
| 2 |
| 1 |
| 2 |
3
| ||
| 4 |
| 1 |
| 2 |
| 1 |
| 16 |
解得x3=x4=
3
| ||
| 4 |
综上所述,当P在线段AC上滑动时,△PCQ的面积不可能为
3
| ||
| 8 |
| 1 |
| 16 |
此时x的值为
3
| ||
| 4 |
3
| ||
| 4 |
点评:本题结合运动类问题考查了一次函数和二次函数的综合应用,考查学生分类讨论,数形结合的数学思想方法.

练习册系列答案
相关题目
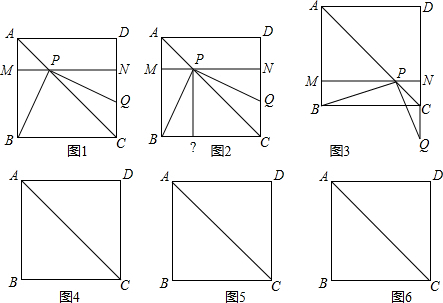
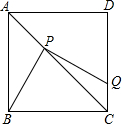 如图,将一把三角尺放在边长为1的正方形ABCD上使它的直角顶点P在对角线AC上滑动,直角的一边始终经过点B,另一边与射线DC相交于点Q,当点Q在边CD上时,线段PQ与线段PB之间有怎样的大小关系?试证明你观察得到的结论.
如图,将一把三角尺放在边长为1的正方形ABCD上使它的直角顶点P在对角线AC上滑动,直角的一边始终经过点B,另一边与射线DC相交于点Q,当点Q在边CD上时,线段PQ与线段PB之间有怎样的大小关系?试证明你观察得到的结论.