题目内容
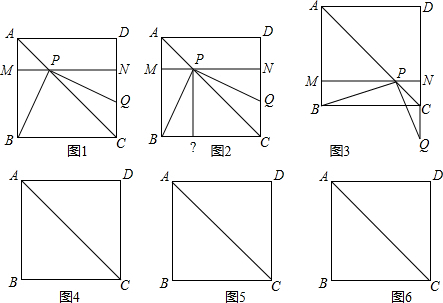
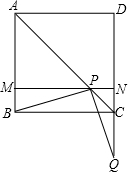
操作:将一把三角尺放在边长为1的正方形ABCD上,并使它的直角顶点P在对角线AC上滑动(点P与点A不重合),直角的一边始终经过点B,直角的另一边与射线DC相交于点Q.探究:设A、P两点的距离为x,问当点P在线段AC上滑动时,△PCQ能否成为等腰三角形:
分析:首先过点P作PF⊥BC于点F,PE⊥CD于点E,易证得四边形PFCE是正方形,设AP=x,CQ=y,易求得当Q在DC上时,y=1-
x,当点Q在边DC的延长线上时,y=
x-1,然后分别分析PC=CQ与PQ=QC时的情景,即可求得答案.
| 2 |
| 2 |
解答:解:能.
理由: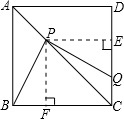
如图,当Q在DC上时,过点P作PF⊥BC于点F,PE⊥CD于点E,
∵∠BCD=90°
∴四边形PFCE是矩形,
∵∠PCE=45°,∠PEQ=90°,
∴PE=EC.
∴四边形PFCE是正方形.
∵AP=x,CQ=y,
∵AB=BC=1,
∴AC=
,
∵四边形PFCE是正方形,
∴PC=
-x,
∴CE=1-
x,
∴BF=1-FC=1-(1-
x)=
x,
∴EQ=
x,
∴y=CQ=(1-
x)-
x=1-
x,
∴y=1-
x(0≤x≤
);
同理:当点Q在边DC的延长线上时,
∵PC=
-x,利用勾股定理得出:EC=1-
x,
EQ=BF=MP=
x,
∴CQ=EQ-EC=
x-1,
∴y=
x-1(
≤x≤
);
∴①当点P与点A重合,点Q与点D重合,这时PQ=QC,△PCQ是等腰三角形,此时x=0;
②当点Q在边DC的延长线上,且CP=CQ时,△PCQ是等腰三角形(如图),此时,QN=PM=
x,CP=
-x,CN=
CP=1-
x,
∴CQ=QN-CN=
x-(1-
x)=
x-1,
当
-x=
x-1时,得x=1.
∴当x=0或1时,△PCQ是等腰三角形.
理由:

如图,当Q在DC上时,过点P作PF⊥BC于点F,PE⊥CD于点E,
∵∠BCD=90°
∴四边形PFCE是矩形,
∵∠PCE=45°,∠PEQ=90°,
∴PE=EC.
∴四边形PFCE是正方形.
∵AP=x,CQ=y,
∵AB=BC=1,
∴AC=
| 2 |
∵四边形PFCE是正方形,
∴PC=
| 2 |
∴CE=1-
| ||
| 2 |
∴BF=1-FC=1-(1-
| ||
| 2 |
| ||
| 2 |
∴EQ=
| ||
| 2 |
∴y=CQ=(1-
| ||
| 2 |
| ||
| 2 |
| 2 |
∴y=1-
| 2 |
| ||
| 2 |
同理:当点Q在边DC的延长线上时,
∵PC=
| 2 |
| ||
| 2 |
EQ=BF=MP=
| ||
| 2 |
∴CQ=EQ-EC=
| 2 |
∴y=
| 2 |
| ||
| 2 |
| 2 |
∴①当点P与点A重合,点Q与点D重合,这时PQ=QC,△PCQ是等腰三角形,此时x=0;
②当点Q在边DC的延长线上,且CP=CQ时,△PCQ是等腰三角形(如图),此时,QN=PM=
| ||
| 2 |
| 2 |
| ||
| 2 |
| ||
| 2 |
∴CQ=QN-CN=
| ||
| 2 |
| ||
| 2 |
| 2 |
当
| 2 |
| 2 |
∴当x=0或1时,△PCQ是等腰三角形.

点评:此题考查正方形的性质,直角三角形的性质,等腰三角形的判定与性质以及一次函数的应用等知识.此题综合性很强,难度较大,解题的关键是注意在正方形中的特殊三角形的应用,搞清楚矩形、菱形、正方形中的三角形的三边关系,可有助于提高解题速度和准确率,注意数形结合思想的应用,注意辅助线的作法.

练习册系列答案
相关题目