题目内容
已知四个实数a,b,c,d,且a≠b,c≠d.若四个关系式:a2+ac=4,b2+bc=4,c2+ac=8,d2+ad=8同时成立,试求a,c的值.
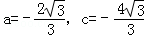
试题分析:此题首先由已知得出a+b+c=0,a+c+d=0,得出b=d,再由(a2+ac)+(c2+ac)=4+8=12,(a2+ac)﹣(c2+ac)=4﹣8=﹣4,得出
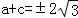 ,(a﹣c)(a+c)=﹣4,然后讨论得出a,c的值.
,(a﹣c)(a+c)=﹣4,然后讨论得出a,c的值.解:由(a2+ac)﹣(b2+bc)=4﹣4=0,(c2+ac)﹣(d2+ad)=8﹣8=0,
得 (a﹣b)(a+b+c)=0,(c﹣d)(a+c+d)=0,
∵a≠b,c≠d,
∴a+b+c=0,a+c+d=0,
∴b=d=﹣(a+c).
又(a2+ac)+(c2+ac)=4+8=12,(a2+ac)﹣(c2+ac)=4﹣8=﹣4,
得
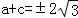 ,(a﹣c)(a+c)=﹣4.
,(a﹣c)(a+c)=﹣4.当
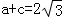 时,
时,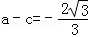 ,
,解得
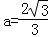 ,
,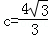 ,
,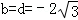
当
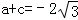 ,
,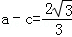 ,
,解得
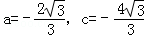 ,
,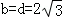 .
.点评:此题考查的知识点是因式分解的应用,通过等式加减及运用因式分解是关键.

练习册系列答案
 步步高达标卷系列答案
步步高达标卷系列答案
相关题目
