题目内容
（2012•台湾）有一个二次函数y=x2+ax+b，其中a、b为整数．已知此函数在坐标平面上的图形与x轴交于两点，且两交点的距离为4．若此图形的对称轴为x=-5，则此图形通过下列哪一点？（ ）
分析：根据二次函数图形的对称轴为x=-5，图形与x轴的两个交点距离为4可知两点的坐标为（-7，0）和（-3，0），设出此函数的解析式，把x=-6代入进行计算即可．
解答：解：∵二次函数图形的对称轴为x=-5，图形与x轴的两个交点距离为4，
∴此两点的坐标为（-7，0）和（-3，0）
设二次函数的解析式为：y=（x+7）（x+3），将x=-6代入，得y=（-6+7）（-6+3）=-3
∴点（-6，-3）在二次函数的图象上．
故选C．
∴此两点的坐标为（-7，0）和（-3，0）
设二次函数的解析式为：y=（x+7）（x+3），将x=-6代入，得y=（-6+7）（-6+3）=-3
∴点（-6，-3）在二次函数的图象上．
故选C．
点评：本题考查的是抛物线与x轴的交点问题，根据题意得出二次函数的交点式是解答此题的关键．
练习册系列答案
相关题目
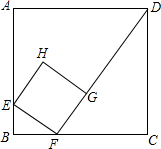（2012•台湾）如图，边长12的正方形ABCD中，有一个小正方形EFGH，其中E、F、G分别在AB、BC、FD上．若BF=3，则小正方形的边长为何？（ ）
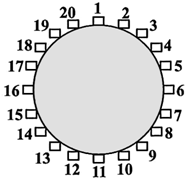（2012•台湾）如图，一圆桌周围有20个箱子，依顺时针方向编号1～20．小明在1号箱子中丢入一颗红球后，沿着圆桌依顺时针方向行走，每经过一个箱子就依下列规则丢入一颗球：
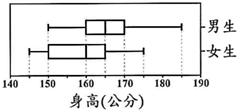（2012•台湾）三年甲班男、女生各有20人，如图为三年甲班男、女生身高的盒状图．若班上每位同学的身高均不相等，则全班身高的中位数在下列哪一个范围？（ ）