题目内容
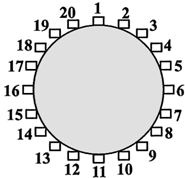 (2012•台湾)如图,一圆桌周围有20个箱子,依顺时针方向编号1~20.小明在1号箱子中丢入一颗红球后,沿着圆桌依顺时针方向行走,每经过一个箱子就依下列规则丢入一颗球:
(2012•台湾)如图,一圆桌周围有20个箱子,依顺时针方向编号1~20.小明在1号箱子中丢入一颗红球后,沿着圆桌依顺时针方向行走,每经过一个箱子就依下列规则丢入一颗球:(1)若前一个箱子丢红球,经过的箱子就丢绿球.
(2)若前一个箱子丢绿球,经过的箱子就丢白球.
(3)若前一个箱子丢白球,经过的箱子就丢红球.
已知他沿着圆桌走了100圈,求4号箱内有几颗红球?( )
分析:根据已知要求得出第1、4、7、…、100圈会在4号箱内丢一颗红球,进而得出通项公式an=a1+(n-1)d,得出答案即可.
解答:解:第1圈红球在1、4、7、10、13、16、19号箱内,
第2圈红球在2、5、8、11、14、17、20号箱内,
第3圈红球在3、6、9、12、15、18号箱内,
第4圈红球在1、4、7、10、13、16、19号箱内,
…
且第1、4、7、…、100圈会在4号箱内丢一颗红球,
an=a1+(n-1)d,
100=1+3(n-1),
33=n-1,
n=34,
故选:B.
第2圈红球在2、5、8、11、14、17、20号箱内,
第3圈红球在3、6、9、12、15、18号箱内,
第4圈红球在1、4、7、10、13、16、19号箱内,
…
且第1、4、7、…、100圈会在4号箱内丢一颗红球,
an=a1+(n-1)d,
100=1+3(n-1),
33=n-1,
n=34,
故选:B.
点评:此题主要考查了图形的变化类,根据已知规律得出通项公式是解题关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 (2012•台湾)如图是利用短除法求出三数8、12、18的最大公因子的过程.利用短除法,求出这三数的最小公倍数为何?( )
(2012•台湾)如图是利用短除法求出三数8、12、18的最大公因子的过程.利用短除法,求出这三数的最小公倍数为何?( ) (2012•台湾)如图,坐标平面上直线L的方程式为3x-y=-3.若有一直线L′的方程式为y=a,则a的值在下列哪一个范围时,L′与L的交点会在第二象限?( )
(2012•台湾)如图,坐标平面上直线L的方程式为3x-y=-3.若有一直线L′的方程式为y=a,则a的值在下列哪一个范围时,L′与L的交点会在第二象限?( )
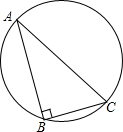 (2012•台湾)如图,直角三角形ABC有一外接圆,其中∠B=90°,AB>BC,今欲在
(2012•台湾)如图,直角三角形ABC有一外接圆,其中∠B=90°,AB>BC,今欲在