题目内容
 操作与探究:
操作与探究:
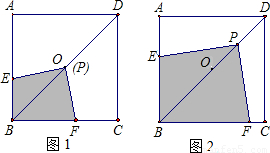
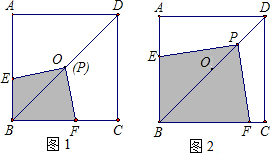
如图1,在正方形ABCD中,AB=2,将一块足够大的三角板的直角顶点P放在正方形的中心O处,将三角板绕O点旋转,三角板的两直角边分别交边AB、BC于点E、F.
(1)试猜想PE、PF之间的大小关系,并证明你的结论;
(2)求四边形PEBF的面积;
(3)现将直角顶点P移至对角线BD上其他任意一点,PE、PF之间的大小关系是否改变?并说明理由.
 解:(1)PE=PF.
解:(1)PE=PF.作PM⊥AB于点M,PN⊥BC于点N.
∵ABCD是正方形,∴BD平分∠ABC.
∴PM=PN.
在四边形BEPF中,
∵∠EBF=∠EPF=90°,
∴∠PFB+∠PEB=180°.
又∵∠PEB+∠PEM=180°,
∴∠PFB=∠PEM.
∴Rt△PEM≌Rt△PFN,(AAS)
∴PE=PF;
(2)由(1)知四边形PEBF的面积等于正方形PMBN的面积.
∵BO=OD,OM∥AD,
∴BM=AM=1.
∴S四边形PEBF=1;
(3)不会改变.理由如下:
作PM⊥AB于点M,PN⊥BC于点N.
∵ABCD是正方形,∴BD平分∠ABC.
∴PM=PN.
在四边形BEPF中,
∵∠EBF=∠EPF=90°,
∴∠PFB+∠PEB=180°.
又∵∠PEB+∠PEM=180°,
∴∠PFB=∠PEM.
∴Rt△PEM≌Rt△PFN,(AAS)
∴PE=PF.
分析:(1)猜想:PE=PF.作PM⊥AB于点M,PN⊥BC于点N.运用AAS证明△PME与△PNF全等;
(2)由(1)可知四边形PEBF的面积等于正方形PMBN的面积;
(3)PE、PF之间的大小关系不会改变.理由同(1).
点评:此题考查正方形的性质及全等三角形的判定与性质,综合性较强.

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目
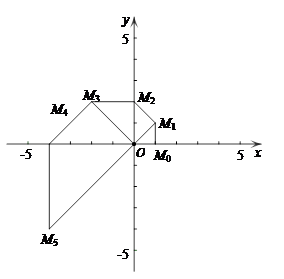
 25、操作与探究:
25、操作与探究: 的坐标为(1,0).将线段
的坐标为(1,0).将线段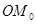 绕原点O沿逆时针方向旋转45
绕原点O沿逆时针方向旋转45 ,再将其延长到
,再将其延长到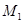 ,使得
,使得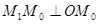 ,得到线段
,得到线段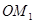 ;又将线段
;又将线段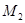 ,使得
,使得 ,得到线段
,得到线段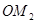 ,如此下去,得到线段
,如此下去,得到线段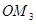 ,
,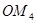 ,…,
,…,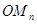 .
.
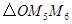 的周长;
的周长; (
(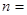 0,1,2,3…)的横坐标
0,1,2,3…)的横坐标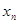 ,纵坐标
,纵坐标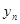 都取绝对值后得到的新坐标
都取绝对值后得到的新坐标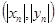 称之为点
称之为点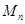 的“绝对坐标”.根据图中点
的“绝对坐标”.根据图中点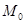 的坐标为(1,0).将线段
的坐标为(1,0).将线段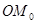 绕原点O沿逆时针方向旋转45
绕原点O沿逆时针方向旋转45 ,再将其延长到
,再将其延长到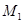 ,使得
,使得 ,得到线段
,得到线段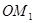 ;又将线段
;又将线段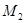 ,使得
,使得 ,得到线段
,得到线段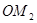 ,如此下去,得到线段
,如此下去,得到线段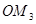 ,
,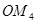 ,…,
,…,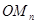 .
.
 的周长;
的周长; (
(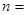 0,1,2,3…)的横坐标
0,1,2,3…)的横坐标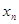 ,纵坐标
,纵坐标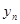 都取绝对值后得到的新坐标
都取绝对值后得到的新坐标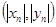 称之为点
称之为点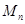 的“绝对坐标”.根据图中点
的“绝对坐标”.根据图中点