题目内容
操作与探究:
如图,在平面直角坐标系xOy中,已知点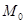 的坐标为(1,0).将线段
的坐标为(1,0).将线段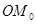 绕原点O沿逆时针方向旋转45
绕原点O沿逆时针方向旋转45 ,再将其延长到
,再将其延长到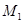 ,使得
,使得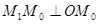 ,得到线段
,得到线段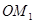 ;又将线段
;又将线段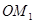 绕原点O沿逆时针方向旋转45
绕原点O沿逆时针方向旋转45 ,再将其延长到
,再将其延长到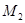 ,使得
,使得 ,得到线段
,得到线段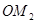 ,如此下去,得到线段
,如此下去,得到线段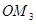 ,
,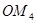 ,…,
,…,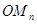 .
.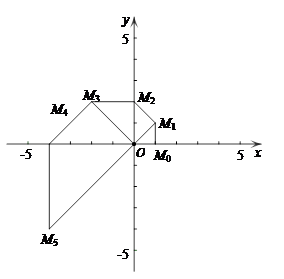
(1)写出点M5的坐标;
(2)求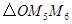 的周长;
的周长;
(3)我们规定:把点 (
(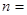 0,1,2,3…)的横坐标
0,1,2,3…)的横坐标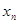 ,纵坐标
,纵坐标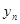 都取绝对值后得到的新坐标
都取绝对值后得到的新坐标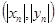 称之为点
称之为点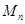 的“绝对坐标”.根据图中点
的“绝对坐标”.根据图中点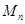 的分布规律,请写出点
的分布规律,请写出点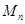 的“绝对坐标”.
的“绝对坐标”.
(1)M5(―4,―4)(2)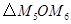 的周长是
的周长是 (3)①当
(3)①当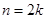 时(其中
时(其中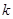 =0,1,2,3,…),点在
=0,1,2,3,…),点在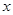 轴上,则
轴上,则 (
( )
)
②当 时(其中
时(其中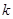 =1,2,3,…),点在
=1,2,3,…),点在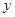 轴上,点
轴上,点 (
( )
)
③当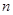 =1,2,3,…,时,点在各象限的分角线上,则点
=1,2,3,…,时,点在各象限的分角线上,则点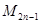 (
( )
)
解析试题分析:解:(1)M5(―4,―4)
(2)由规律可知, ,
, ,
,
∴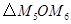 的周长是
的周长是
(3)解法一:由题意知,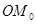 旋转8次之后回到
旋转8次之后回到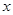 轴的正半轴,在这8次旋转中,点
轴的正半轴,在这8次旋转中,点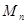 分别落在坐标象限的分角线上或
分别落在坐标象限的分角线上或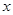 轴或
轴或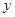 轴上,但各点“绝对坐标”的横、纵坐标均为非负数,因此,点
轴上,但各点“绝对坐标”的横、纵坐标均为非负数,因此,点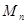 的“绝对坐标”可分三类情况:
的“绝对坐标”可分三类情况:
令旋转次数为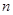
① 当点M在x轴上时: M0(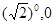 ),M4(
),M4( ),M8(
),M8(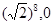 ),M12(
),M12( ),…,
),…,
即:点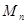 的“绝对坐标”为(
的“绝对坐标”为( )。
)。
② 当点M在y轴上时: M2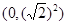 ,M6
,M6 ,M10
,M10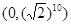 ,M14
,M14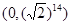 ,……,
,……,
即:点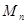 的“绝对坐标”为
的“绝对坐标”为 .
.
③ 当点M在各象限的分角线上时:M1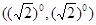 ,M3
,M3 ,M5
,M5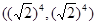 ,M7
,M7 ,即:
,即: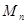 的“绝对坐标”为
的“绝对坐标”为 .
.
解法二:由题意知,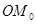 旋转8次之后回到
旋转8次之后回到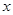 轴的正半轴,在这8次旋转中,点分别落在坐标象限的分角线上或
轴的正半轴,在这8次旋转中,点分别落在坐标象限的分角线上或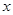 轴或
轴或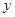 轴上,但各点“绝对坐标”的横、纵坐标均为非负数,因此,各点的“绝对坐标”可分三种情况:
轴上,但各点“绝对坐标”的横、纵坐标均为非负数,因此,各点的“绝对坐标”可分三种情况:
①当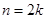 时(其中
时(其中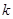 =0,1,2,3,…),点在
=0,1,2,3,…),点在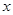 轴上,则
轴上,则 (
( )
)
②当 时(其中
时(其中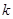 =1,2,3,…),点在
=1,2,3,…),点在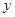 轴上,点
轴上,点 (
( )
)
③当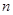 =1,2,3,…,时,点在各象限的分角线上,则点
=1,2,3,…,时,点在各象限的分角线上,则点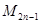 (
( )
)
考点:探究规律题型
点评:本题难度较大,主要考查学生对几何题型综合探究规律综合运用的掌握。为中考常考题型,要求学生多做探究训练,总结分析规律,运用到考试中去。

 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案 25、操作与探究:
25、操作与探究:
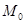 的坐标为(1,0).将线段
的坐标为(1,0).将线段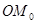 绕原点O沿逆时针方向旋转45
绕原点O沿逆时针方向旋转45 ,再将其延长到
,再将其延长到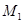 ,使得
,使得 ,得到线段
,得到线段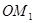 ;又将线段
;又将线段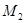 ,使得
,使得 ,得到线段
,得到线段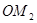 ,如此下去,得到线段
,如此下去,得到线段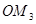 ,
,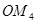 ,…,
,…,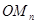 .
.
 的周长;
的周长; (
(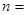 0,1,2,3…)的横坐标
0,1,2,3…)的横坐标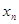 ,纵坐标
,纵坐标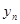 都取绝对值后得到的新坐标
都取绝对值后得到的新坐标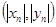 称之为点
称之为点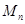 的“绝对坐标”.根据图中点
的“绝对坐标”.根据图中点