题目内容
【题目】如图1,已知线段AB两个端点坐标分别为A(a,0),B(0,b),且a,b满足:![]()
(1)填空:a= ,b= .

(2)在坐标轴上是否存在点C,使S△ABC=6,若存在,求出点C的坐标,符不存在,说明理由;
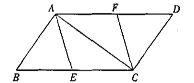
(3)如图2,若将线段Ba平移得到线段OD,其中B点对应O点,A点对应D点,点P(m,n)是线段OD上任意一点,请直接写出m与n的关系式。
【答案】(1) -6,4;(2) C坐标为(-9,0),(-3,0),(0,2),(0,6);(3)2m=3n(-6≤m≤0).
【解析】
(1)根据非负数的性质列方程求解即可;
(2)根据点B的坐标,求出B到x轴的距离,再利用三角形的面积求出AC的长度,然后分点C在A点的左边和右边两种情况讨论求解;
(3)根据平移求出点D的坐标,然后求出OD的解析式,再把P点的坐标代入求解即可.
解:(1)∵![]()
∴a=-6,b=4,
故答案为-6,4;
(2)由(1)知,a=-6,b=4,
∴A(-6,0),B(0,4),
当点C在x轴上时,设C(c,0),
∴AC=|c+6|,
∵S△ABC=6,![]()
∴c=-9或c=-3,
∴C(-9,0)或(-3,0),
当点C在y轴上时,设C(0,c'),
∴BC=|c'-4|,
∵S△ABC=6,![]()
∴c'=2或c'=6,
∴C(0,2)或(0,6),
即:满足条件的点C坐标为(-9,0),(-3,0),(0,2),(0,6);
(3)由(2)知,A(-6,0),B(0,4),
∵将线段BA平移得到线段OD,其中B点对应O点,A点对应D,
∴线段AB向下平移4个单位到线段OD,
∴D(-6,-4),设线段OD所在直线解析式为y=kx,
∴-6k=-4,

【题目】随着手机的普及,微信![]() 一种聊天软件
一种聊天软件![]() 的兴起,许多人抓住这种机会,做起了“微商”,很多农产品也改变了原来的销售模式,实行了网上销售,这不刚大学毕业的小明把自家的冬枣产品也放到了网上,他原计划每天卖100斤冬枣,但由于种种原因,实际每天的销售量与计划量相比有出入,下表是某周的销售情况
的兴起,许多人抓住这种机会,做起了“微商”,很多农产品也改变了原来的销售模式,实行了网上销售,这不刚大学毕业的小明把自家的冬枣产品也放到了网上,他原计划每天卖100斤冬枣,但由于种种原因,实际每天的销售量与计划量相比有出入,下表是某周的销售情况![]() 超额记为正,不足记为负
超额记为正,不足记为负![]() 单位:斤
单位:斤![]() ;
;
星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
与计划量的差值 |
|
|
|
|
|
|
|
(1)根据记录的数据可知前三天共卖出 ______ 斤;
(2)根据记录的数据可知销售量最多的一天比销售量最少的一天多销售 ______ 斤;
(3)本周实际销售总量达到了计划数量没有?
(4)若冬季每斤按8元出售,每斤冬枣的运费平均3元,那么小明本周一共收入多少元?