题目内容
我们把分子为1的分数叫做理想分数,如 ,
, ,
, ,…,任何一个理想分数都可以写成两个不同理想分数的和,如
,…,任何一个理想分数都可以写成两个不同理想分数的和,如 =
= +
+ ;
; =
= +
+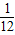 ;
; =
= +
+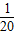 ;…根据对上述式子的观察,请你思考:如果理想分数
;…根据对上述式子的观察,请你思考:如果理想分数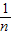 (n是不小于2的正整数)=
(n是不小于2的正整数)=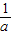 +
+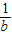 ,那么a+b= .(用含n的式子表示)
,那么a+b= .(用含n的式子表示)
【答案】分析:根据题意,分析可得在 =
= +
+ ,有(2+1)2=3+6;在
,有(2+1)2=3+6;在 =
= +
+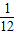 ,有(3+1)2=4+12;如果理想分数
,有(3+1)2=4+12;如果理想分数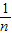 =
=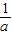 +
+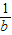 ,那么a+b=(n+1)2.
,那么a+b=(n+1)2.
解答:解:a+b=(n+1)2.
点评:本题考查学生通过观察、归纳、抽象出数列的规律的能力,要求学生首先分析题意,找到规律,并进行推导得出答案.
 =
= +
+ ,有(2+1)2=3+6;在
,有(2+1)2=3+6;在 =
= +
+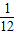 ,有(3+1)2=4+12;如果理想分数
,有(3+1)2=4+12;如果理想分数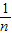 =
=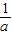 +
+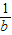 ,那么a+b=(n+1)2.
,那么a+b=(n+1)2.解答:解:a+b=(n+1)2.
点评:本题考查学生通过观察、归纳、抽象出数列的规律的能力,要求学生首先分析题意,找到规律,并进行推导得出答案.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目