题目内容
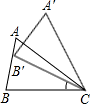如图，把△ABC绕C点顺时针旋转35°，得△A′B′C，此时恰好A′B′⊥AC，则∠A′=
- A.35°
- B.55°
- C.60°
- D.65°
B
分析：由旋转角为35°可知，∠ACA′=35°，又AC⊥A′B′，可判断∠A′与∠ACA′互余，根据互余关系求∠A′，根据对应角相等求∠A．
解答：由旋转角为35°可知，∠ACA′=35°，
又∵AC⊥A′B′，
∴∠A′+∠ACA′=90°，
∴∠A′=90°-∠ACA′=55°，
∴∠A=∠A′=55°．
故选B．
点评：本题考查了旋转的性质．关键是明确图形中的旋转角，对应角，两角之间的互余关系．
分析：由旋转角为35°可知，∠ACA′=35°，又AC⊥A′B′，可判断∠A′与∠ACA′互余，根据互余关系求∠A′，根据对应角相等求∠A．
解答：由旋转角为35°可知，∠ACA′=35°，
又∵AC⊥A′B′，
∴∠A′+∠ACA′=90°，
∴∠A′=90°-∠ACA′=55°，
∴∠A=∠A′=55°．
故选B．
点评：本题考查了旋转的性质．关键是明确图形中的旋转角，对应角，两角之间的互余关系．
练习册系列答案
相关题目
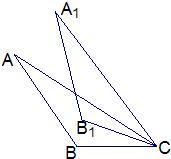14、如图，把△ABC绕点C顺时针旋转22度，得△A1B1C，则直线AB与A1B1所成的锐角为
（2013•沁阳市一模）如图，把△ABC绕着点C顺时针旋转30°，得到△A′B′C，A′B′交AC于点D，若∠A′DC=90°，则∠A的度数是（ ）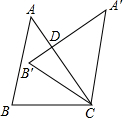
如图，把△ABC绕点C顺时针旋转43°，得到△A′B′C，A′B′交AC于点D，若∠A′DC=90°，则∠A=
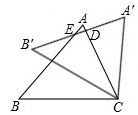如图，把△ABC绕点C顺时针旋转25°，得到△A′B′C′，A′B′分别交AC、AB于点D、E，若∠A′DC=80°，则∠A=