题目内容
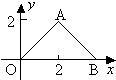 (2005•湘潭)如图,在△AOB中,AO=AB,在直角坐标系中,点A的坐标是(2,2),点O的坐标是(0,0),将△AOB平移得到△A′O′B′,使得点A′在y轴上.点O′、B′在x轴上.则点B'的坐标是
(2005•湘潭)如图,在△AOB中,AO=AB,在直角坐标系中,点A的坐标是(2,2),点O的坐标是(0,0),将△AOB平移得到△A′O′B′,使得点A′在y轴上.点O′、B′在x轴上.则点B'的坐标是(2,0)
(2,0)
.分析:直接利用平移中点的变化规律求解即可.
平移中点的变化规律是:横坐标右移加,左移减;纵坐标上移加,下移减.
平移中点的变化规律是:横坐标右移加,左移减;纵坐标上移加,下移减.
解答:解:∵AO=AB,点A的横坐标为2,
∴OB=4,B的坐标为(4,0),
要想让点O'、B'还在x轴上,只能左右平移.
∵点A的坐标是(2,2),移动到y轴上时,坐标变为(0,2),说明点A向左平了2个单位,即横坐标减2,
∴B点也遵循点A的移动规律,则点B'的坐标是(2,0).
故答案填:(2,0).
∴OB=4,B的坐标为(4,0),
要想让点O'、B'还在x轴上,只能左右平移.
∵点A的坐标是(2,2),移动到y轴上时,坐标变为(0,2),说明点A向左平了2个单位,即横坐标减2,
∴B点也遵循点A的移动规律,则点B'的坐标是(2,0).
故答案填:(2,0).
点评:解决本题的关键是得到三角形的平移方法,需注意只有左右移动才改变点的横坐标,左减,右加.

练习册系列答案
相关题目
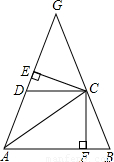
 上一点,则∠ACB= 度.
上一点,则∠ACB= 度.