ĢāÄæÄŚČŻ
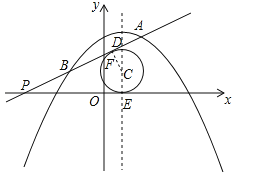
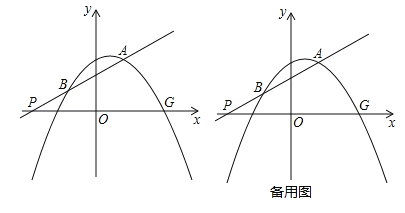
”¾ĢāÄæ”æČēĶ¼£¬¶ž“ĪŗÆŹży=©![]() x2+mx+nµÄĶ¼Ļó¾¹żµćA£Ø2£¬3£©£¬ÓėxÖįµÄÕż°ėÖį½»ÓŚµćG£Ø1+
x2+mx+nµÄĶ¼Ļó¾¹żµćA£Ø2£¬3£©£¬ÓėxÖįµÄÕż°ėÖį½»ÓŚµćG£Ø1+![]() £¬0£©£»Ņ»“ĪŗÆŹży=kx+bµÄĶ¼Ļó¾¹żµćA£¬ĒŅ½»xÖįÓŚµćP£¬½»Å×ĪļĻßÓŚĮķŅ»µćB£¬ÓÖÖŖµćA£¬BĪ»ÓŚµćPµÄĶ¬²ą£®
£¬0£©£»Ņ»“ĪŗÆŹży=kx+bµÄĶ¼Ļó¾¹żµćA£¬ĒŅ½»xÖįÓŚµćP£¬½»Å×ĪļĻßÓŚĮķŅ»µćB£¬ÓÖÖŖµćA£¬BĪ»ÓŚµćPµÄĶ¬²ą£®
£Ø1£©ĒóÕāøö¶ž“ĪŗÆŹżµÄ½āĪöŹ½£»
£Ø2£©ČōPA=3PB£¬ĒóŅ»“ĪŗÆŹżµÄ½āĪöŹ½£»
£Ø3£©ŌŚ£Ø2£©µÄĢõ¼žĻĀ£¬µ±k£¾0Ź±£¬Å×ĪļĻߵĶŌ³ĘÖįÉĻŹĒ·ń“ęŌŚµćC£¬Ź¹”ŃCĶ¬Ź±ÓėxÖįŗĶÖ±ĻßAP¶¼ĻąĒŠ£æČē¹ū“ęŌŚ£¬ĒėĒó³öµćCµÄ×ų±ź£»Čē¹ū²»“ęŌŚ£¬ĒėĖµĆ÷ĄķÓÉ£®
”¾“š°ø”æ£Ø1£©![]() £»£Ø2£©
£»£Ø2£© ![]() »ņ
»ņ![]() £» £Ø3£©“ęŌŚÕāŃłµÄµć
£» £Ø3£©“ęŌŚÕāŃłµÄµć![]() »ņ£Ø1£¬©5
»ņ£Ø1£¬©5![]() ©10£©£¬Ź¹µĆ
©10£©£¬Ź¹µĆ![]() Ķ¬Ź±Óė
Ķ¬Ź±Óė![]() ÖįŗĶÖ±Ļß
ÖįŗĶÖ±Ļß![]() ¶¼ĻąĒŠ£®
¶¼ĻąĒŠ£®
”¾½āĪö”æ·ÖĪö£ŗ£Ø1£©øł¾ŻÅ×ĪļĻߵĶŌ³ĘÖįĪŖx=1æÉĒó³ömµÄÖµ£¬ŌŁ½«µćAµÄ×ų±ź“śČėÅ×ĪļĻߵĽāĪöŹ½ÖŠĒó³önÖµ£¬“ĖĢāµĆ½ā£»
£Ø2£©øł¾ŻP”¢A”¢BČżµć¹²ĻßŅŌ¼°PA=3PB½įŗĻµćAµÄ×ų±ź¼“æÉµĆ³öµćBµÄׯ×ų±ź£¬½«Ęä“śČėÅ×ĪļĻß½āĪöŹ½ÖŠ¼“æÉĒó³öµćBµÄ×ų±ź£¬ŌŁøł¾ŻµćA”¢BµÄ×ų±źĄūÓĆ“ż¶ØĻµŹż·Ø¼“æÉĒó³öÖ±ĻßAPµÄ½āĪöŹ½£»
£Ø3£©¼ŁÉč“ęŌŚ£¬Éč³öµćCµÄ×ų±ź£¬ŅĄÕÕĢāŅā»³öĶ¼ŠĪ£¬øł¾Ż½ĒµÄ¼ĘĖćÕŅ³ö”ĻDCF=”ĻEPF£¬ŌŁĶعż½āÖ±½ĒČż½ĒŠĪÕŅ³ö¹ŲÓŚrµÄŅ»ŌŖŅ»“Ī·½³Ģ£¬½ā·½³ĢĒó³örÖµ£¬½«Ęä“śČėµćCµÄ×ų±źÖŠ¼“æÉµĆ³ö½įĀŪ£®
Ļź½ā£ŗ£Ø1£©”ßÅ×ĪļĻߵĶŌ³ĘÖįĪŖx=1£¬”ą©![]() =1£¬½āµĆ£ŗm=
=1£¬½āµĆ£ŗm=![]() £®
£®
½«µćA£Ø2£¬3£©“śČėy=©![]() x2+
x2+![]() x+nÖŠ£¬3=©1+1+n£¬½āµĆ£ŗn=3£¬”ąÅ×ĪļĻߵĽāĪöŹ½ĪŖy=©
x+nÖŠ£¬3=©1+1+n£¬½āµĆ£ŗn=3£¬”ąÅ×ĪļĻߵĽāĪöŹ½ĪŖy=©![]() x2+
x2+![]() x+3£®
x+3£®
£Ø2£©”ßP”¢A”¢BČżµć¹²Ļߣ¬PA=3PB£¬ĒŅµćA”¢BĪ»ÓŚµćPµÄĶ¬²ą£¬”ąyA©yP=3£ØyB©yP£©£®
Ó֔ߵćPĪŖxÖįÉĻµÄµć£¬µćA£Ø2£¬3£©£¬”ąyB=1£®
µ±y=1Ź±£¬ÓŠ©![]() x2+
x2+![]() x+3=1£¬½āµĆ£ŗx1=©2£¬x2=4£¬”ąµćBµÄ×ų±źĪŖ£Ø©2£¬1£©»ņ£Ø4£¬1£©£®
x+3=1£¬½āµĆ£ŗx1=©2£¬x2=4£¬”ąµćBµÄ×ų±źĪŖ£Ø©2£¬1£©»ņ£Ø4£¬1£©£®
½«µćA£Ø2£¬3£©”¢B£Ø©2£¬1£©“śČėy=kx+bÖŠµĆ![]() £¬½āµĆ£ŗ
£¬½āµĆ£ŗ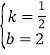 £¬”ąŅ»“ĪŗÆŹżµÄ½āĪöŹ½y=
£¬”ąŅ»“ĪŗÆŹżµÄ½āĪöŹ½y=![]() x+2£»
x+2£»
½«µćA£Ø2£¬3£©”¢B£Ø4£¬1£©“śČėy=kx+bÖŠ![]() £¬½āµĆ£ŗ
£¬½āµĆ£ŗ![]() £¬”ąŅ»“ĪŗÆŹżµÄ½āĪöŹ½y=©x+5£®
£¬”ąŅ»“ĪŗÆŹżµÄ½āĪöŹ½y=©x+5£®
×ŪÉĻĖłŹö£ŗµ±PA£ŗPB=3£ŗ1Ź±£¬Ņ»“ĪŗÆŹżµÄ½āĪöŹ½ĪŖy=![]() x+2»ņy=©x+5£®
x+2»ņy=©x+5£®
£Ø3£©¼ŁÉč“ęŌŚ£¬ÉčµćCµÄ×ų±źĪŖ£Ø1£¬r£©£®
”ßk£¾0£¬”ąÖ±ĻßAPµÄ½āĪöŹ½ĪŖy=![]() x+2£®
x+2£®
µ±y=0Ź±£¬![]() x+2=0£¬½āµĆ£ŗx=©4£¬”ąµćPµÄ×ų±źĪŖ£Ø©4£¬0£©£¬µ±x=1Ź±£¬y=
x+2=0£¬½āµĆ£ŗx=©4£¬”ąµćPµÄ×ų±źĪŖ£Ø©4£¬0£©£¬µ±x=1Ź±£¬y=![]() £¬”ąµćDµÄ×ų±źĪŖ£Ø1£¬
£¬”ąµćDµÄ×ų±źĪŖ£Ø1£¬![]() £©£®
£©£®
Įī”ŃÓėÖ±ĻßAPµÄĒŠµćĪŖF£¬ÓėxÖįµÄĒŠµćĪŖE£¬Å×ĪļĻߵĶŌ³ĘÖįÓėÖ±ĻßAPµÄ½»µćĪŖD£¬Į¬½ÓCF£¬ČēĶ¼ĖłŹ¾£®
”ß”ĻPFC=”ĻPEC=90”ć£¬”ĻEPF+”ĻECF=”ĻDCF+”ĻECF=180”ć£¬”ą”ĻDCF=”ĻEPF£®
ŌŚRt”÷CDFÖŠ£¬tan”ĻDCF=tan”ĻEPF=![]() £¬CD=
£¬CD=![]() ©r£¬”ąCD=
©r£¬”ąCD=![]() CF=
CF=![]() |r|=
|r|=![]() ©r£¬½āµĆ£ŗr=
©r£¬½āµĆ£ŗr=![]() ©10»ņr=©5
©10»ņr=©5![]() ©10£®
©10£®
¹Źµ±k£¾0Ź±£¬Å×ĪļĻߵĶŌ³ĘÖįÉĻ“ęŌŚµćC£¬Ź¹µĆ”ŃCĶ¬Ź±ÓėxÖįŗĶÖ±ĻßAP¶¼ĻąĒŠ£¬µćCµÄ×ų±źĪŖ£Ø1£¬5![]() ©10£©»ņ£Ø1£¬©5
©10£©»ņ£Ø1£¬©5![]() ©10£©£®
©10£©£®