题目内容
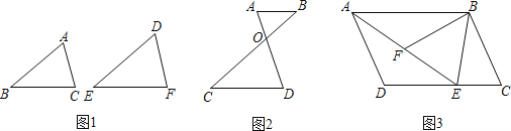
【题目】 先阅读下面的材料,再解答下面的问题:如果两个三角形的形状相同,则称这两个三角形相似.如图1,△ABC与△DEF形状相同,则称△ABC与△DEF相似,记作△ABC∽△DEF.那么,如何说明两个三角形相似呢?我们可以用“两角分别相等的三角形相似”加以说明.用数学语言表示为:
如图1:在△ABC与△DEF中,∵∠A=∠D,∠B=∠E,∴△ABC∽△DEF.
请你利用上述定理解决下面的问题:
(1)下列说法:①有一个角为50°的两个等腰三角形相似;②有一个角为100°的两个等腰三角形相似;③有一个锐角相等的两个直角三角形相似;④两个等边三角形相似.其中正确的是______(填序号);
(2)如图2,已知AB∥CD,AD与BC相交于点O,试说明△ABO∽△DCO;
(3)如图3,在平行四边形ABCD中,E是DC上一点,连接AE.F为AE上一点,且∠BFE=∠C,求证:△ABF∽△EAD.
【答案】(1)②③④;(2)见解析;(3)见解析
【解析】
(1)由于50°的角可作为等腰三角形的顶角,也可以作为底角,由此可判断①;而100°的角只能作为等腰三角形的顶角,故可判断②;根据直角三角形的性质可判断③;根据等边三角形的性质可判断④,进而可得答案;
(2)根据平行线的性质和材料提供的方法解答即可;
(3)根据平行四边形的性质和平行线的性质可得∠BAE=∠AED,∠D+∠C=180°,然后根据已知和补角的性质可得∠D=∠AFB,进而可得结论.
解:(1)①由于50°的角可作为等腰三角形的顶角,也可以作为底角,所以有一个角为50°的两个等腰三角形不一定相似,所以①错误;
②由于100°的角只能作为等腰三角形的顶角,所以有一个角为100°的两个等腰三角形一定相似,所以②正确;
③有一个锐角相等的两个直角三角形一定相似,所以③正确;
④两个等边三角形一定相似,所以④正确.
故答案为②③④;
(2)∵AB∥CD,∴∠A=∠D,∠B=∠C,
∴△ABO∽△DCO;
(3)证明:∵四边形ABCD是平行四边形,
∴AB∥CD,AD∥BC,
∴∠BAE=∠AED,∠D+∠C=180°,
∵∠AFB+∠BFE=180°,∠BFE=∠C,
∴∠D=∠AFB,
∴△ABF∽△EAD.


 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案【题目】为了了解某市九年级学生的体育成绩(成绩均为整数),随机抽取了部分学生的体育成绩并分段(A:20.5~22.5;B:22.5~24.5;C:24.5~26.5;D:26.5~28.5;E:28.5~30.5)统计如下,而且制成了如图所示的不完整的统计图.
体育成绩统计表
分数段 | 频数 | 频率 |
A | 12 | 0.05 |
B | 36 | a |
C | 84 | 0.35 |
D | b | 0.25 |
E | 48 | 0.20 |
体育成绩统计图

根据上面提供的信息,解答下列问题:
(1)在统计表中,a=________,b=________,并将统计图补充完整;
(2)小明说:“这组数据的众数一定在C中.”你认为小明的说法正确吗?__________(填“正确”或“错误”).
(3)若成绩在27分以上(含27分)定为优秀,则该市今年48 000名九年级学生中体育成绩为优秀的学生约有多少?