题目内容
(2009•金华)在平面直角坐标系中,O为坐标原点.(1)已知点A(3,1),连接OA,平移线段OA,使点O落在点B.设点A落在点C,作如下探究:
探究一:若点B的坐标为(1,2),请在图1中作出平移后的像,则点C的坐标是______;连接AC,BO,请判断O,A,C,B四点构成的图形的形状,并说明理由;
探究二:若点B的坐标为(6,2),按探究一的方法,判断O,A,B,C四点构成的图形的形状.
(温馨提示:作图时,别忘了用黑色字迹的钢笔或签字笔描黑喔!)
(2)通过上面的探究,请直接回答下列问题:
①若已知三点A(a,b),B(c,d),C(a+c,b+d),顺次连接O,A,C,B,请判断所得到的图形的形状;
②在①的条件下,如果所得到的图形是菱形或者是正方形,请选择一种情况,写出a,b,c,d应满足的关系式.

【答案】分析:(1)由题意和图象可知:OA应该右移三个单位,上移两个单位后得出的C因此,C的坐标是(4,3).因为是平移所以AO=BC,AO∥BC,所以四边形OACB是平行四边形.当B是(6,2)的时候,OAB三点在直线y= x上,因此OABC是条线段.
x上,因此OABC是条线段.
(2)①同(1)应该是平行四边形或线段两种情况.
②当OACB是菱形时,两条邻边应该相等,AC=BC,因此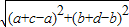 =
= ,因此a2+b2=c2+d2,
,因此a2+b2=c2+d2,
当OACB是正方形的时候.如果过B作BE⊥x轴,过A作AF⊥x轴,那么三角形BOE≌三角形AOF.AF=OE,OF=BE,即A点的横坐标的绝对值=B点的横坐标的绝对值,A点的纵坐标的绝对值=B点的纵坐标的绝对值,即a=d且b=-c或b=c且a=-d.
解答:解:

(1)探究一:C(4,3),
四边形OACB为平行四边形,
理由如下:
由平移可知,OA∥BC,且OA=BC,
所以四边形OACB为平行四边形.
探究二:线段
(2)①平行四边形或线段;
②菱形:a2+b2=c2+d2(a=-c,b=-d除外)
正方形:a=d且b=-c或b=c且a=-d.
(写出菱形需满足的条件或写出正方形需满足的条件其中一种即可给分)
点评:本题考查图形的平移变换.关键是要懂得左右平移点的纵坐标不变,而上下平移时点的横坐标不变.
 x上,因此OABC是条线段.
x上,因此OABC是条线段.(2)①同(1)应该是平行四边形或线段两种情况.
②当OACB是菱形时,两条邻边应该相等,AC=BC,因此
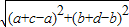 =
= ,因此a2+b2=c2+d2,
,因此a2+b2=c2+d2,当OACB是正方形的时候.如果过B作BE⊥x轴,过A作AF⊥x轴,那么三角形BOE≌三角形AOF.AF=OE,OF=BE,即A点的横坐标的绝对值=B点的横坐标的绝对值,A点的纵坐标的绝对值=B点的纵坐标的绝对值,即a=d且b=-c或b=c且a=-d.
解答:解:

(1)探究一:C(4,3),
四边形OACB为平行四边形,
理由如下:
由平移可知,OA∥BC,且OA=BC,
所以四边形OACB为平行四边形.
探究二:线段
(2)①平行四边形或线段;
②菱形:a2+b2=c2+d2(a=-c,b=-d除外)
正方形:a=d且b=-c或b=c且a=-d.
(写出菱形需满足的条件或写出正方形需满足的条件其中一种即可给分)
点评:本题考查图形的平移变换.关键是要懂得左右平移点的纵坐标不变,而上下平移时点的横坐标不变.

练习册系列答案
相关题目