题目内容
（2004•武汉）已知：如图，在⊙O的内接四边形ABCD中，AB是直径，∠BCD=130°，过D点的切线PD与直线AB交于P点，则∠ADP的度数为（ ）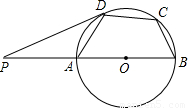
A．40°
B．45°
C．50°
D．65°
【答案】分析：连接BD，由圆内接四边形的对角互补，AB是直径知∠DAB=180°-∠C=50°，∠ADB=90°，所以可求∠ABD=40°；再根据PD是切线，弦切角定理知，∠ADP=∠B=40°．
解答：
解：连接BD，
∵∠DAB=180°-∠C=50°，AB是直径，
∴∠ADB=90°，∠ABD=90°-∠DAB=40°，
∵PD是切线，
∴∠ADP=∠B=40°．
故选A．
点评：本题利用了圆内接四边形的性质，直径对圆周角等于直角，弦切角定理，弦切角等于它所夹的弧对的圆周角求解．
解答：
解：连接BD，∵∠DAB=180°-∠C=50°，AB是直径，
∴∠ADB=90°，∠ABD=90°-∠DAB=40°，
∵PD是切线，
∴∠ADP=∠B=40°．
故选A．
点评：本题利用了圆内接四边形的性质，直径对圆周角等于直角，弦切角定理，弦切角等于它所夹的弧对的圆周角求解．
练习册系列答案
相关题目