题目内容
为了了解某校1000名初中生右眼视力情况,随机对50名学生右眼视力进行了检查,绘制了如下统计表和频率分布直方图.| 视力 | 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 | 0.7 | 0.8 |
| 人数 | 1 | 1 | 3 | 2 | 3 | 4 | 2 | |
| 视力 | 0.9 | 1.0 | 1.1 | 1.2 | 1.3 | 1.4 | 1.5 | |
| 人数 | 2 | 4 | 8 | 4 | 2 | 6 |
(1)补全统计表和频率分布直方图;
(2)填空:在这个问题中,样本是______,在这个样本中,视力的中位数是______,视力的众数落在频率分布直方图(从左至右依次是第一、二、三、四、五小组)的______小组内.
(3)如果右眼视力在0.6及0.6以下的必须矫正,试估计该校右眼视力必须矫正的学生约有多少人?

【答案】分析:(1)根据统计表与统计图中的原有数据补全即可.
(2)根据样本,中位数,众数的概念即可解答.
(3)利用用样本估计总体的方法计算即可.
解答:解:(1)
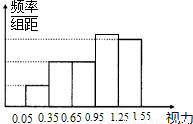
(2)∵随机对50名学生右眼视力进行了检查,
∴样本为50名学生右眼视力情况,
中位数为25与25名学生的平均数,为1.0,
视力的众数为1.2,落在第四小组内.
(3)右眼视力在0.6及0.6以下的人数为14,概率为14÷50=0.28,所以该校右眼视力必须矫正的学生约有1000×0.28=280人.
点评:本题考查读频数分布直方图的能力和利用统计图获取信息的能力;利用统计图获取信息时,必须认真观察、分析、研究统计图,才能作出正确的判断和解决问题.本题用到的知识点是:将一组数据从小到大依次排列,把中间数据(或中间两数据的平均数)叫做中位数.频率=频数÷总数,用样本估计整体让整体×样本的百分比即可.
(2)根据样本,中位数,众数的概念即可解答.
(3)利用用样本估计总体的方法计算即可.
解答:解:(1)
| 视力 | 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 | 0.7 | 0.8 |
| 人数 | 1 | 1 | 3 | 2 | 3 | 4 | 2 | 5 |
| 视力 | 0.9 | 1.0 | 1.1 | 1.2 | 1.3 | 1.4 | 1.5 | |
| 人数 | 2 | 4 | 3 | 8 | 4 | 2 | 6 |

(2)∵随机对50名学生右眼视力进行了检查,
∴样本为50名学生右眼视力情况,
中位数为25与25名学生的平均数,为1.0,
视力的众数为1.2,落在第四小组内.
(3)右眼视力在0.6及0.6以下的人数为14,概率为14÷50=0.28,所以该校右眼视力必须矫正的学生约有1000×0.28=280人.
点评:本题考查读频数分布直方图的能力和利用统计图获取信息的能力;利用统计图获取信息时,必须认真观察、分析、研究统计图,才能作出正确的判断和解决问题.本题用到的知识点是:将一组数据从小到大依次排列,把中间数据(或中间两数据的平均数)叫做中位数.频率=频数÷总数,用样本估计整体让整体×样本的百分比即可.

练习册系列答案
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
相关题目

 22、为了了解某校1000名初中生右眼视力情况,随机对50名学生右眼视力进行了检查,绘制了如下统计表和频率分布直方图.
22、为了了解某校1000名初中生右眼视力情况,随机对50名学生右眼视力进行了检查,绘制了如下统计表和频率分布直方图.