题目内容
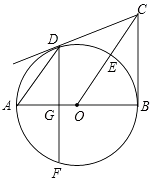
【题目】如图:矩形ABCD中AB=2,BC= ![]() ,⊙A是以A为圆心,半径r=1的圆,若⊙A绕着点B顺时针旋转,旋转角为α( 0°<α<180°);当旋转后的圆与矩形ABCD的边相切时,α=度.
,⊙A是以A为圆心,半径r=1的圆,若⊙A绕着点B顺时针旋转,旋转角为α( 0°<α<180°);当旋转后的圆与矩形ABCD的边相切时,α=度. 
【答案】60或120
【解析】解:
∵⊙A是以A为圆心,半径r=1的圆,AB=2,
∴当圆在矩形内部时,则与AD、BC都相切,
设与BC的切点为E,此时圆心为A′,连接A′E、A′B,如图,
则在Rt△A′BE中,A′E=1,A′B=AB=2,
∴∠A′BE=30°,
∴∠A′BA=90°﹣30°=60°;
当圆在矩形外部与BC相切时,设圆心为A″,
同理可求得∠A″BE=30°,
∴∠A″BA=90°+30°=120°;
综上可知α=60°或120°,
所以答案是:60或120.
【考点精析】根据题目的已知条件,利用矩形的性质和切线的性质定理的相关知识可以得到问题的答案,需要掌握矩形的四个角都是直角,矩形的对角线相等;切线的性质:1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径.

练习册系列答案
 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案
相关题目