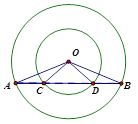
题目内容
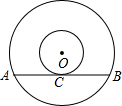如图，在同心圆中，大圆的弦AB切小圆于点C，AB=8，则圆环的面积是（ ）分析：连接OA，OC，根据切线的性质和勾股定理可得：OA2-OC2=（
AB）2，写出环形的面积表达式，把数值代入即可．
| 1 |
| 2 |
解答：解：连接OA，OC，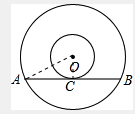
∵大圆中长为8的弦AB与小圆相切，
∴OC⊥AB，AC=4，
∴OA2-OC2=16，
∴πOA2-πOC2=（OA2-OC2）π，
∴圆环的面积=16π．
故选C．
∵大圆中长为8的弦AB与小圆相切，
∴OC⊥AB，AC=4，
∴OA2-OC2=16，
∴πOA2-πOC2=（OA2-OC2）π，
∴圆环的面积=16π．
故选C．
点评：本题主要考查了圆形的面积公式、切线的性质、垂径定理，关键在于作好辅助线，求环形面积表达式．
练习册系列答案
开心蛙状元测试卷系列答案
相关题目
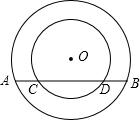如图，在同心圆中，大圆的弦AB与小圆相交于点C，D，且AC=CD=DB，若两圆的半径分别为4cm和2cm，则CD的长等于（ ）| A、3cm | ||
| B、2.5cm | ||
C、
| ||
D、
|
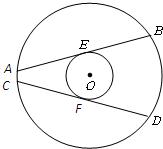35、已知：如图，在同心圆中，大圆的弦AB，CD分别与小圆相切于点E，F，则弦AB，CD的大小关系是（ ）
已知：如图，在同心圆中，大圆的弦AB交小圆于C、D两点．