Question

（本小题10分）如图11，已知二次函数y= -x² +mx +4m的图象与x轴交于

A(x₁，0)，B(x₂，0)两点(B点在A点的右边)，与y轴的正半轴交于点C，且(x₁+x₂) - x₁x₂=10.

（1）求此二次函数的解析式.

（2）写出B，C两点的坐标及抛物线顶点M的坐标；

（3）连结BM，动点P在线段BM上运动（不含端点B，M），过点P作x轴的垂线，垂足为H，设OH的长度为t，四边形PCOH的面积为S.请探究：四边形PCOH的面积S有无最大值？如果有，请求出这个最大值；如果没有，请说明理由.

 

Answer 1

解：（1）由根与系数的关系，得

∵(x₁+x₂) -x₁x₂=10，

∴m + 4m =10，m=2.

∴二次函数的解析式为y = -x² +2x +8.

（2）由-x²+2x +8=0，解得x₁= -2，x₂=4.

y = -x² +2x +8=-(x-1)²+9.

∴B，C，M的坐标分别为B(4，0)，C(0，8)，M(1，9).

（3）如图，过M作MN⊥x轴于N，则ON=1，MN=9，OB=4，BN=3.

∵OH=t(1<t<4)，∴BH=4-t.

由PH∥MN，可求得PH=3BH=3(4-t)，

∴S=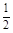(PH+CO)·OH

=(12-3t+8)t

= -t²+10t(1<t<4).

S= -t²+10t= -(t-)²+.

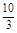∵1<<4.

∴当t=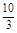时，S有最大值，其最大值为.

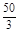解析:略