题目内容
(本小题10分)如图, 抛物线 与x轴的一个交点是A,与y轴的交点是B,且OA、OB(OA<OB)的长是方程
与x轴的一个交点是A,与y轴的交点是B,且OA、OB(OA<OB)的长是方程 的两个实数根.
的两个实数根.

1.(1)求A、B两点的坐标;
2. (2) 求出此抛物线的的解析式及顶点D的坐标;
3.(3)求出此抛物线与x轴的另一个交点C的坐标;
4.(4)在直线BC上是否存在一点P,使四边形PDCO为梯形?若存在,求出P点坐标,若不存在,说明理由.
【答案】
1.解:(1)∵ 的两个实数根为
的两个实数根为
OA、OB(OA<OB)的长是方程 的两个实数根
的两个实数根
∴ OA=1,OB=5
∴ A(1,0), B(0,5)
2.(2)∵抛物线 与x轴的一个交点是A,与y轴的交点是B
与x轴的一个交点是A,与y轴的交点是B
∴
解得:
∴所求二次函数的解析式为: -------------------------3分
-------------------------3分
顶点坐标为:D(-2,9)
3.(3)此抛物线与x轴的另一个交点C的坐标为(-5,0)
4.(4)直线CD的解析式为:
y=3x+15 --------------------------6分
直线BC的解析式为:
y=x+5 ---------------------------7分
①若以CD为底,则OP∥CD
直线OP的解析式为:y=3x
 于是有
于是有 解得:
解得:
∴点P的坐标为( --------------8分
--------------8分
②若以OC为底,则DP∥CO
直线DP的解析式为:y=9
于是有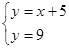 解得:
解得:
∴点P的坐标为(4,9) --------------------------9分
∴在直线BC上存在点P,使四边形PDCO为梯形且P点坐标为( 或
或
(4,9)
【解析】略

练习册系列答案
 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案
相关题目

 与x轴交与A(1,0),B(- 3,0)两点,
与x轴交与A(1,0),B(- 3,0)两点,
