题目内容
(本题12分)
某商品的进价为每千克40元,销售单价与月销售量的关系如下表(每千克售价不能高于65元):
|
销售单价(元) |
50 |
53 |
56 |
59 |
62 |
65 |
|
月销售量(千克) |
420 |
360 |
300 |
240 |
180 |
120 |
该商品以每千克50元为售价,在此基础上设每千克的售价上涨 元(
元( 为正整数),每个月的销售利润为
为正整数),每个月的销售利润为 元.
元.
(1)求 与
与 的函数关系式,并直接写出自变量
的函数关系式,并直接写出自变量 的取值范围;
的取值范围;
(2)每千克商品的售价定为多少元时,每个月可获得最大利润?最大的月利润是多少元?
y=-20x2+220x+4200( 且
且 为整数);
为整数);
(2)当售价定为每件55或56元,每个月的利润最大,最大的月利润是4800元.
【解析】
试题分析:
(1)由表数据可知,在每千克50元售价基础上,每上涨3元,月销售量减少60千克,易知,每上涨1元时,月销售量减少20千克。所以涨价后每千克的利润为(420-20x)元,月销售量为(50+x-40)千克。列式得y=(420-20x)(50+x-40)=-20x2+220x+4200( 且
且 为整数);
为整数);
(2)y=-20x2+220x+4200=-20(x-5.5)2+4805.
∵a=-20<0, 当
当 时,
时,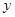 有最大值4805.
有最大值4805.
 ,且
,且 为整数,
为整数,
当 时,
时, ,y=4800(元),当
,y=4800(元),当 时,
时, ,y=4800(元)
,y=4800(元)
∴当售价定为每件55或56元,每个月的利润最大,最大的月利润是4800元.
考点:二次函数的实际应用
点评:难度中等。本题考查学生对二次函数的实际问题的列式运算。遇到要求y的最大值时,有时候需要把二次函数式 化简为带完全平方的式子。完全平方公式:a2+2ab+b2=(a+b)2
化简为带完全平方的式子。完全平方公式:a2+2ab+b2=(a+b)2

(本题12分)某商场购进一批单价为5元的日用商品.如果以单价7元销售,每天可售出160件.根据销售经验,提高销售单价会导致销售量的减少,即销售单价每提高1元,销售量每天就相应减少20件.设这种商品的销售单价为x元,商品每天销售这种商品所获得的利润为y元.
(1)给定x的一些值,请计算y的一些值.
| x | … | 7 | 8 | 9 | 10 | 11 | … |
| y | … |
|
|
|
|
| … |
(2)求y与x之间的函数关系式,并探索:当商品的销售单价定为多少元时,该商店销售这种商品获得的利润最大?这时每天销售的商品是多少件?
(本题12分)某商场购进一批单价为5元的日用商品.如果以单价7元销售,每天可售出160件.根据销售经验,提高销售单价会导致销售量的减少,即销售单价每提高1元,销售量每天就相应减少20件.设这种商品的销售单价为x元,商品每天销售这种商品所获得的利润为y元.
(1)给定x的一些值,请计算y的一些值.
| x | … | 7 | 8 | 9 | 10 | 11 | … |
| y | … | | | | | | … |
 的一部
的一部
 元交费.
元交费. )
)