题目内容
【题目】如图1,已知CF是△ABC的外角∠ACE的角平分线,D为CF上一点,且DA=DB.

(1)求证:∠ACB=∠ADB;
(2)求证:AC+BC<2BD;
(3)如图2,若∠ECF=60°,证明:AC=BC+CD.
【答案】(1)详见解析;(2)详见解析;(3)详见解析.
【解析】
(1)过点D分别作AC,CE的垂线,垂足分别为M,N,证明Rt△DAM≌Rt△DBN,得出∠DAM=∠DBN,则结论得证;
(2)证明Rt△DMC≌Rt△DNC,可得CM=CN,得出AC+BC=2BN,又BN<BD,则结论得证;
(3)在AC上取一点P,使CP=CD,连接DP,可证明△ADP≌△BDC,得出AP=BC,则结论可得出.
(1)证明:过点D分别作AC,CE的垂线,垂足分别为M,N,
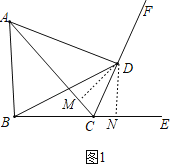
∵CF是△ABC的外角∠ACE的角平分线,
∴DM=DN,
在Rt△DAM和Rt△DBN中,
![]() ,
,
∴Rt△DAM≌Rt△DBN(HL),
∴∠DAM=∠DBN,
∴∠ACB=∠ADB;
(2)证明:由(1)知DM=DN,
在Rt△DMC和Rt△DNC中,
![]() ,
,
∴Rt△DMC≌Rt△DNC(HL),
∴CM=CN,
∴AC+BC=AM+CM+BC=AM+CN+BC=AM+BN,
又∵AM=BN,
∴AC+BC=2BN,
∵BN<BD,
∴AC+BC<2BD.
(3)由(1)知∠CAD=∠CBD,在AC上取一点P,使CP=CD,
连接DP,
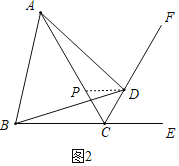
∵∠ECF=60°,∠ACF=60°,
∴△CDP为等边三角形,
∴DP=DC,∠DPC=60°,
∴∠APD=120°,
∵∠ECF=60°,
∴∠BCD=120°,
在△ADP和△BDC中,
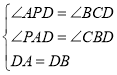 ,
,
∴△ADP≌△BDC(AAS),
∴AP=BC,
∵AC=AP+CP,
∴AC=BC+CP,
∴AC=BC+CD.

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目