Question

如图所示，若AB∥CD，AP，CP分别平分∠BAC和∠ACD，PE⊥AC于E，且PE=3cm，则AB与CD之间的距离为（ ）
A．3cm
B．6cm
C．9cm
D．无法确定

Answer 1

【答案】分析：过点P作pM⊥AB，并反向延长交CD于点N，根据平行线的性质及全等三角形的判定定理可得出△AED≌△AMD，CPE≌△CPN，即可得出结论．
解答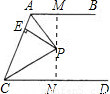：解：过点P作pM⊥AB，并反向延长交CD于点N，
∵AB∥CD，则PN⊥CD，
在△AED和△AMD中，
∵∠BAC=∠ACD，
∠AED=∠AMD，
AD=AD，
∴△AED≌△AMD（AAS），
∴PM=PE=3cm，
在△CPE和△CPN中，
∵∠ECP=∠PCN，
∠PNC=∠PEC，
 PC=PC，
∴△CPE≌△CPN（AAS），
∴PN=PE=3CM，
∴MN=PM+PN=3+3=6cm，
∴AB与CD之间的距离是6cm．
故选B．
点评：本题考查的是平行线的性质及全等三角形的判定与性质，根据题意作出辅助线，构造出全等三角形是解答此题的关键．