题目内容
【题目】如图,一次函数y=kx+b的图象与坐标轴分别交于A、B两点,与反比例函数y= ![]() 的图象在第一象限的交点为C,CD⊥x轴,垂足为D,若OB=3,OD=6,△AOB的面积为3.
的图象在第一象限的交点为C,CD⊥x轴,垂足为D,若OB=3,OD=6,△AOB的面积为3. 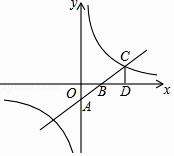
(1)求一次函数与反比例函数的解析式;
(2)直接写出当x>0时,kx+b﹣ ![]() <0的解集.
<0的解集.
【答案】
(1)解:∵S△AOB=3,OB=3,
∴OA=2,
∴B(3,0),A(0,﹣2),
代入y=kx+b得: ![]() ,
,
解得:k= ![]() ,b=﹣2,
,b=﹣2,
∴一次函数y= ![]() x﹣2,
x﹣2,
∵OD=6,
∴D(6,0),CD⊥x轴,
当x=6时,y= ![]() ×6﹣2=2
×6﹣2=2
∴C(6,2),
∴n=6×2=12,
∴反比例函数的解析式是y= ![]() ;
;
(2)解:当x>0时,kx+b﹣ ![]() <0的解集是0<x<6.
<0的解集是0<x<6.
【解析】(1)根据三角形面积求出OA,得出A、B的坐标,代入一次函数的解析式即可求出解析式,把x=6代入求出D的坐标,把D的坐标代入反比例函数的解析式求出即可;(2)根据图象即可得出答案.

练习册系列答案
相关题目
【题目】甲、乙两运动员的射击成绩(靶心为10环)统计如下表(不完全):
次数 | 1 | 2 | 3 | 4 | 5 |
甲 | 10 | 8 | 9 | 10 | 8 |
乙 | 10 | 9 | 9 | a | b |
某同学计算出了甲的成绩平均数是9,方差是
S甲2= ![]() [(10﹣9)2+(8﹣9)2+(9﹣9)2+(10﹣9)2+(8﹣9)2]=0.8,请作答:
[(10﹣9)2+(8﹣9)2+(9﹣9)2+(10﹣9)2+(8﹣9)2]=0.8,请作答: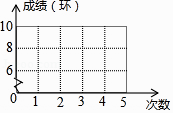
(1)在图中用折线统计图将甲运动员的成绩表示出来;
(2)若甲、乙射击成绩平均数都一样,则a+b=;
(3)在(2)的条件下,当甲比乙的成绩较稳定时,请列举出a、b的所有可能取值,并说明理由.