题目内容
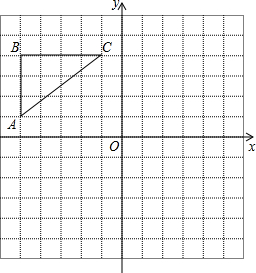 (2013•海南)如图,在正方形网格中,△ABC各顶点都在格点上,点A,C的坐标分别为(-5,1)、(-1,4),结合所给的平面直角坐标系解答下列问题:
(2013•海南)如图,在正方形网格中,△ABC各顶点都在格点上,点A,C的坐标分别为(-5,1)、(-1,4),结合所给的平面直角坐标系解答下列问题:(1)画出△ABC关于y轴对称的△A1B1C1;
(2)画出△ABC关于原点O对称的△A2B2C2;
(3)点C1的坐标是
(1,4)
(1,4)
;点C2的坐标是(1,-4)
(1,-4)
;过C、C1、C2三点的圆的圆弧 |
| CC1C2 |
| 17 |
| 17 |
分析:(1)根据网格结构找出点A、B、C关于y轴的对称点A1、B1、C1的位置,然后顺次连接即可;
(2)根据网格结构找出点A、B、C关于原点的对称点A2、B2、C2的位置,然后顺次连接即可;
(3)根据平面直角坐标系写出点C1、C2的坐标,利用勾股定理求出OC的长,再根据过C、C1、C2三点的圆的圆弧是以CC2为直径的半圆,列式计算即可得解.
(2)根据网格结构找出点A、B、C关于原点的对称点A2、B2、C2的位置,然后顺次连接即可;
(3)根据平面直角坐标系写出点C1、C2的坐标,利用勾股定理求出OC的长,再根据过C、C1、C2三点的圆的圆弧是以CC2为直径的半圆,列式计算即可得解.
解答: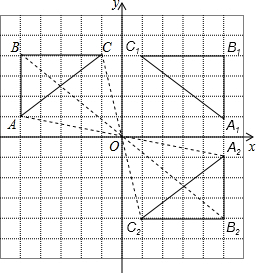 解:(1)△A1B1C1如图所示;
解:(1)△A1B1C1如图所示;
(2)△A2B2C2如图所示;
(3)C1(1,4),C2(1,-4),
根据勾股定理,OC=
=
,
过C、C1、C2三点的圆的圆弧是以CC2为直径的半圆,
的长=
π.
故答案为:(1,4);(1,-4);
π.
 解:(1)△A1B1C1如图所示;
解:(1)△A1B1C1如图所示;(2)△A2B2C2如图所示;
(3)C1(1,4),C2(1,-4),
根据勾股定理,OC=
| 12+42 |
| 17 |
过C、C1、C2三点的圆的圆弧是以CC2为直径的半圆,
 |
| CC1C2 |
| 17 |
故答案为:(1,4);(1,-4);
| 17 |
点评:本题考查了利用旋转变换作图,利用轴对称变换作图,以及弧长的计算,熟练掌握网格结构,准确找出对应点的位置是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
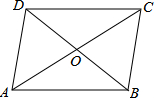 (2013•海南)如图,在?ABCD中,AC与BD相交于点O,则下列结论不一定成立的是( )
(2013•海南)如图,在?ABCD中,AC与BD相交于点O,则下列结论不一定成立的是( )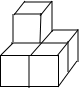 (2013•海南)如图是由5个大小相同的正方体组成的几何体,它的俯视图为( )
(2013•海南)如图是由5个大小相同的正方体组成的几何体,它的俯视图为( )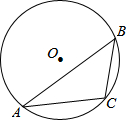 (2013•海南)如图,在⊙O中,弦BC=1.点A是圆上一点,且∠BAC=30°,则⊙O的半径是( )
(2013•海南)如图,在⊙O中,弦BC=1.点A是圆上一点,且∠BAC=30°,则⊙O的半径是( )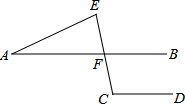 (2013•海南)如图,AB∥CD,AE=AF,CE交AB于点F,∠C=110°,则∠A=
(2013•海南)如图,AB∥CD,AE=AF,CE交AB于点F,∠C=110°,则∠A=