题目内容
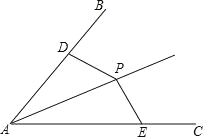
【题目】如图，在等腰
中，
，AD是
的角平分线，且
，以点A为圆心，AD长为半径画弧EF，交AB于点E，交AC于点F．
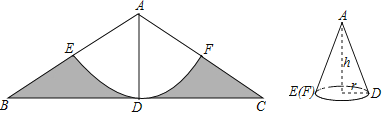
（1）求由弧EF及线段FC、CB、BE围成图形（图中阴影部分）的面积；
（2）将阴影部分剪掉，余下扇形AEF，将扇形AEF围成一个圆锥的侧面，AE与AF正好重合，圆锥侧面无重叠，求这个圆锥的高h．
【答案】（1）
；（2）
.
【解析】
（1）利用等腰三角形的性质得到
，
，则可计算出
，然后利用扇形的面积公式，利用由弧EF及线段FC、CB、BE围成图形（图中阴影部分）的面积
进行计算；（2）设圆锥的底面圆的半径为r，利用圆锥的侧面展开图为一扇形，这个扇形的弧长等于圆锥底面的周长，扇形的半径等于圆锥的母线长和弧长公式得到
，解得
，然后利用勾股定理计算这个圆锥的高h．
∵在等腰
中，
，
∴
，
∵AD是
的角平分线，
∴，，
∴
，
∴
，
∴由弧EF及线段FC、CB、BE围成图形（图中阴影部分）的面积
.
（2）设圆锥的底面圆的半径为r，
根据题意得，解得，
这个圆锥的高
．
天天向上一本好卷系列答案
小学生10分钟应用题系列答案【题目】某校为了解七年级学生的体重情况，随机抽取了七年级m名学生进行调查，将抽取学生的体重情况绘制如下不完整的频数分布表和扇形统计图．
组别 | 体重（千克） | 人数 |
A | 37.5≤x＜42.5 | 10 |
B | 42.5≤x＜47.5 | n |
C | 47.5≤x＜52.5 | 40 |
D | 52.5≤x＜57.5 | 20 |
E | 57.5≤x＜62.5 | 10 |
请根据图表信息回答下列问题：
（1）填空：①m=_____，②n=_____，③在扇形统计图中，C组所在扇形的圆心角的度数等于_______度；
（2）若把每组中各个体重值用这组数据的中间值代替（例如：A组数据中间值为40千克），则被调查学生的平均体重是多少千克？
（3）如果该校七年级有1000名学生，请估算七年级体重低于47.5千克的学生大约有多少人？
