题目内容
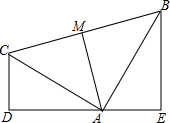 如图所示,已知∠CDA=∠AEB=90°,且CD=AE,AD=BE.问:
如图所示,已知∠CDA=∠AEB=90°,且CD=AE,AD=BE.问:(1)AC与AB相等吗?清说明理由;
(2)△ABC是什么三角形?请说明理由;
(3)如果AM⊥BC,则AM=
| 1 | 2 |
分析:(1)AC=AB,可通过证明△ADC≌△AEB得到;
(2)△ABC是等腰直角三角形,由(1)可知△ABC是等腰三角形,再证明∠CAB=90°即可;
(3)AM=
BC,根据等腰三角形的性质:三线合一证明即可.
(2)△ABC是等腰直角三角形,由(1)可知△ABC是等腰三角形,再证明∠CAB=90°即可;
(3)AM=
| 1 |
| 2 |
解答:解:(1)AC=AB,
理由如下:
在△ADC和△AEB中,
,
∴△ADC≌△AEB,
∴AC=AB;
(2)△ABC是等腰直角三角形,
理由如下:
∵△ADC≌△AEB,
∴∠CDB=∠ABE,
∵∠ABE+∠EAB=90°,
∴∠CAD+∠BAE=90°,
∴∠CAB=90°,
∵AC=BC,
∴△ABC是等腰直角三角形;
(3)AM=
BC,
理由如下:
∵△ABC是等腰直角三角形,AM⊥BC,
∴AM=
BC.
理由如下:
在△ADC和△AEB中,

|
∴△ADC≌△AEB,
∴AC=AB;
(2)△ABC是等腰直角三角形,
理由如下:
∵△ADC≌△AEB,
∴∠CDB=∠ABE,
∵∠ABE+∠EAB=90°,
∴∠CAD+∠BAE=90°,
∴∠CAB=90°,
∵AC=BC,
∴△ABC是等腰直角三角形;
(3)AM=
| 1 |
| 2 |
理由如下:
∵△ABC是等腰直角三角形,AM⊥BC,
∴AM=
| 1 |
| 2 |
点评:本题考查了全等三角形的判定和性质、等腰三角形的判定和性质,题目比较简单.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
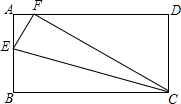 在一次数学活动课上,张明同学将矩形ABCD沿直线CE折叠,顶点B恰好落在AD边上F点处,如图所示,已知CD=8cm,BE=5cm,则AD=
在一次数学活动课上,张明同学将矩形ABCD沿直线CE折叠,顶点B恰好落在AD边上F点处,如图所示,已知CD=8cm,BE=5cm,则AD= 5、如图所示,已知CD⊥AB于点D,BE⊥AC于点E,要使△ABE与△ACD全等,下列给出的条件不正确的是( )
5、如图所示,已知CD⊥AB于点D,BE⊥AC于点E,要使△ABE与△ACD全等,下列给出的条件不正确的是( ) 23、如图所示,已知CD⊥AB,BE⊥AC,垂足分别为D、E、BE、CD相交于O点,∠1=∠2,
23、如图所示,已知CD⊥AB,BE⊥AC,垂足分别为D、E、BE、CD相交于O点,∠1=∠2, 如图所示,已知CD平分∠ACB,DE∥BC,∠AED=5O°,求∠EDC的度数.
如图所示,已知CD平分∠ACB,DE∥BC,∠AED=5O°,求∠EDC的度数. 如图所示,已知CD⊥DA,DA⊥AB,∠1=∠2.
如图所示,已知CD⊥DA,DA⊥AB,∠1=∠2.