题目内容
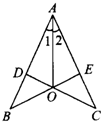23、如图所示，已知CD⊥AB，BE⊥AC，垂足分别为D、E、BE、CD相交于O点，∠1=∠2，（1）写出图中所有全等的三角形；
（2）从（1）中选出一组加以证明．
分析：（1）根据全等三角形的判定定理判断即可；
（2）选择△ADO≌△AEO，根据ASA证明即可．
（2）选择△ADO≌△AEO，根据ASA证明即可．
解答：解：（1）图中所有全等的三角形有：△ADO≌△AEO，△BOD≌△COE，△ABO≌△ACO，△AEB≌△ADC．
（2）证明△ADO≌△AEO，
证明：∵，∠ADO=∠AEO=90°∠1=∠2，AO=AO，
∴△ADO≌△AEO．
（2）证明△ADO≌△AEO，
证明：∵，∠ADO=∠AEO=90°∠1=∠2，AO=AO，
∴△ADO≌△AEO．
点评：本题考查三角形全等的判定方法，判定两个三角形全等的一般方法有：SSS、SAS、ASA、AAS、HL．注意：AAA、SSA不能判定两个三角形全等，判定两个三角形全等时，必须有边的参与，若有两边一角对应相等时，角必须是两边的夹角．
练习册系列答案
相关题目
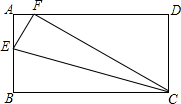在一次数学活动课上，张明同学将矩形ABCD沿直线CE折叠，顶点B恰好落在AD边上F点处，如图所示，已知CD=8cm，BE=5cm，则AD=
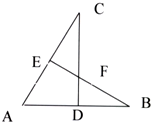5、如图所示，已知CD⊥AB于点D，BE⊥AC于点E，要使△ABE与△ACD全等，下列给出的条件不正确的是（ ）
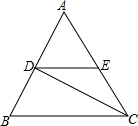如图所示，已知CD平分∠ACB，DE∥BC，∠AED=5O°，求∠EDC的度数．
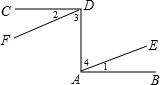如图所示，已知CD⊥DA，DA⊥AB，∠1=∠2．