题目内容
已知:抛物线y1=x2以点C为顶点且过点B,抛物线y2=a2x2+b2x+c2以点B为顶点且过点C,分别过点B、C作x轴的平行线,交抛物线y1=x2、y2=a2x2+b2x+c2于点D,且AB=AC.
(1)如图,①求证△ABC为正三角形;②求点A的坐标;
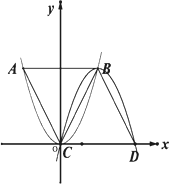
(2)①如图,若将抛物线“y1=x2”改为“y1=x2+1”,其他条件不变,求CD的长;

②如图,若将抛物线“y1=x2”改为“y1=3x2+b1x+c1”,其他条件不变,求a2的值;

(3)若将抛物线“y1=x2”改为抛物线“y1=a1x2+b1x+c1”,其他条件不变,直接写出b1关于b2的关系式.
答案:
解析:
解析:
|
(1)略 (2) (3) |

练习册系列答案
相关题目
 (a≠0)的顶点M的坐标为(1,-2)与y轴交于点C(0,
(a≠0)的顶点M的坐标为(1,-2)与y轴交于点C(0,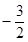 ),与x轴交于A、B两点(A在B的左边).
),与x轴交于A、B两点(A在B的左边).
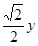 1,求y1与x的函数关系式,并写出自变量x的取值范围;
1,求y1与x的函数关系式,并写出自变量x的取值范围;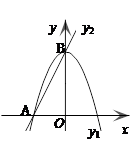
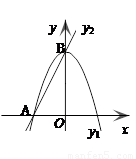
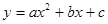 (a≠0)的顶点M的坐标为(1,-2)与y轴交于点C(0,
(a≠0)的顶点M的坐标为(1,-2)与y轴交于点C(0,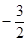 ),与x轴交于A、B两点(A在B的左边).
),与x轴交于A、B两点(A在B的左边).
 1,求y1与x的函数关系式,并写出自变量x的取值范围;
1,求y1与x的函数关系式,并写出自变量x的取值范围;