题目内容
【题目】如图,中间用相同的白色正方形瓷砖,四周用相同的黑色长方形瓷砖铺设矩形地面,请观察图形并解答下列问题:
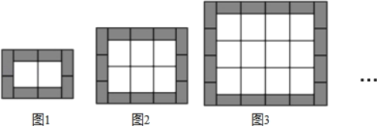
(1)问:依据规律在第n个图中,黑色瓷砖多少块,白色瓷砖有多少块;
(2)问:依据规律在第8个图中,黑色瓷砖多少块,白色瓷砖有多少块;
(3)某新学校教室要装修,每间教室面积为68m2,准备定制边长为0.5米的正方形白色瓷砖和长为0.5米、宽为0.25米的长方形黑色瓷砖来铺地面.按照此图案方式进行装修,瓷砖无须切割,恰好完成铺设.已知白色瓷砖每块20元,黑色瓷砖每块10元,请问每间教室瓷砖共需要多少元?
【答案】(1)黑色瓷砖的块数可以用含有n的代数式表示为:4(n+1),白色瓷砖的块数用含有n的代数式表示为n(n+1);(2)黑色瓷砖:36块;白色瓷砖:72块;(3)每间教室瓷砖共需要5540元.
【解析】
(1)通过观察发现规律得出黑色瓷砖的块数可用含n的代数式表示为4(n+1),白瓷砖的块数可用含n的代数式表示为n(n+1),由此即可得答案;
(2)根据(1)中的规律,将n=8代入计算即可;
(3)设白色瓷砖的行数为n,根据教室的面积,利用矩形的面积公式列方程进行求解即可.
(1)通过观察图形可知,当n=1时,黑色瓷砖有8块,白色瓷砖有2块;
当n=2时,黑色瓷砖有12块,白色瓷砖有6块;当n=3时,黑色瓷砖有16块,白色瓷砖有12块;
发现黑色的瓷砖每次增加4块;而白色的瓷砖第次的数量分别为1×2;2×3;3×4…
则在第n个图形中,黑色瓷砖的块数可以用含有n的代数式表示为:4(n+1),白色瓷砖的块数用含有n的代数式表示为n(n+1);
(2)当n=8时,黑色瓷砖:4×(8+1)=36块;白色瓷砖:8×(8+1)=72块;
(3)设白色瓷砖为行数为n,根据题意,得:0.52×n(n+1)+0.5×0.25×4(n+1)=68
解得n1=15,n2=﹣18 (不合题意,舍去)
白色瓷砖的块数为15×16=240 (块)
黑色瓷砖的块数为4×16=64 (块)
所以每间教室的瓷砖共需要:20×240+10×64=5440 (元)
答:每间教室瓷砖共需要5540元