题目内容
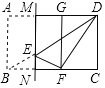
【题目】如图1,在正方形ABCD中,AB=3,E是AD边上的一点(E与A、D不重合),以BE为边画正方形BEFG,边EF与边CD交于点H.
(1)当E为边AD的中点时,求DH的长;
(2)设DE=x,CH=y,求y与x之间的函数关系式,并求出y的最小值;
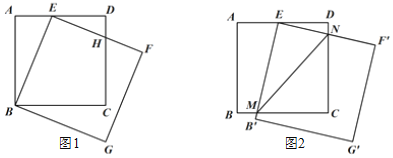
(3)若DE=![]() ,将正方形BEFG绕点E逆时针旋转适当角度后得到正方形B'EF'G',如图2,边EF'与CD交于点N、EB'与BC交于点M,连结MN,求∠ENM的度数.
,将正方形BEFG绕点E逆时针旋转适当角度后得到正方形B'EF'G',如图2,边EF'与CD交于点N、EB'与BC交于点M,连结MN,求∠ENM的度数.
【答案】(1)DH=![]() ; (2)
; (2) ![]() ,y的最小值为
,y的最小值为![]() ;(3)∠ENM=60°.
;(3)∠ENM=60°.
【解析】
(1)根据正方形的性质得到∠D=∠A=∠BEF=90°,根据余角的性质得到∠AEB=∠DHE,根据相似三角形的想知道的![]() ,代入数据即可得到结论;
,代入数据即可得到结论;
(2) 由第一题的比值代入得![]() ,化简整理成二次函数即可,再求出函数的极值;
,化简整理成二次函数即可,再求出函数的极值;
(3)通过作辅助线,可证△PMC∽△PDE, △PCE∽△PMN,得到∠EMN=∠ECN,从而可在△CED中,求得tan∠ECD值,从而求得∠ECD 角度,∠EMN=∠ECD=30°,所以在Rt△EMN中,利用互余求∠ENM=90°-30°=60°.
∵四边形ABCD和四边形BGFE是正方形,
∴∠D=∠A=∠BEF=90°,
∴∠AEB+∠DEH=∠DEH+∠DHE=90°,
∴∠AEB=∠DHE,
∴△EDH∽△BAE,
∴![]() ,
,
∵E为边AD的中点,
∴DE=AE=1.5,
∴![]() ,
,
∴DH=![]() .
.
由上得,![]() ,
,
∴![]() ,
,
∴![]() (2分)=
(2分)=![]() .
.
∵![]() >0,
>0,
∴y的最小值为![]() .
.
(3)
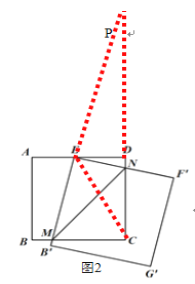
连结CE,延长ME、CD,两线交于点P,
∵在正方形ABCD中,AD∥BC
∴△PMC∽△PED,
∴![]()
变换得:![]()
又∵在Rt△PEN中,![]()
∴![]()
又∵∠P=∠P公共角
∴△PCE∽△PMN,
∴∠EMN=∠ECN
又∵在Rt△CED中,求得tan∠ECD=![]() =
=![]() ,
,
∴∠ECD=30°
∴∠EMN=∠ECD=30°,
∴在Rt△EMN中,∠ENM=90-30°=60°.

 阅读快车系列答案
阅读快车系列答案【题目】一次安全知识测验中,学生得分均为整数,满分10分,成绩达到9分为优秀,这次测验中甲、乙两组学生人数相同,成绩如下两个统计图:
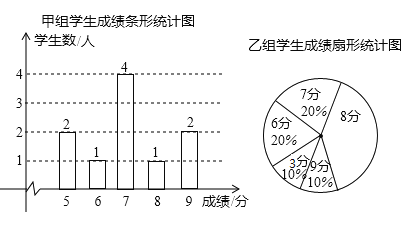
(1)在乙组学生成绩统计图中,8分所在的扇形的圆心角为 度;
(2)请补充完整下面的成绩统计分析表:
平均分 | 方差 | 众数 | 中位数 | 优秀率 | |
甲组 | 7 | 1.8 | 7 | 7 | 20% |
乙组 | 10% |
(3)甲组学生说他们的优秀率高于乙组,所以他们的成绩好于乙组,但乙组学生不同意甲组学生的说法,认为他们组的成绩要好于甲组,请你给出两条支持乙组学生观点的理由.
【题目】某区为了解全区2800名九年级学生英语口语考试成绩的情况,从中随机抽取了部分学生的成绩(满分24分,得分均为整数),制成下表:
分数段(x分) | x≤16 | 17≤x≤18 | 19≤x≤20 | 21≤x≤22 | 23≤x≤24 |
人 数 | 10 | 15 | 35 | 112 | 128 |
(1)填空:
①本次抽样调查共抽取了 名学生;
②学生成绩的中位数落在 分数段;
③若用扇形统计图表示统计结果,则分数段为x≤16的人数所对应扇形的圆心角为 °;
(2)如果将21分以上(含21分)定为优秀,请估计该区九年级考生成绩为优秀的人数.