题目内容
13.设x+y+z=0,则x($\frac{1}{y}$+$\frac{1}{z}$)+y($\frac{1}{z}$+$\frac{1}{x}$)+z($\frac{1}{x}$+$\frac{1}{y}$)+3的值为( )| A. | 0 | B. | -1 | C. | 1 | D. | 2 |
分析 先将原式化简为$\frac{x+z}{y}$+$\frac{x+y}{z}$+$\frac{y+z}{x}$+3,然后根据x+y+z=0,求出x+z=-y,x+y=-z,y+z=-x,代入求解求值即可.
解答 解:原式=$\frac{x}{y}$+$\frac{x}{z}$+$\frac{y}{z}$+$\frac{y}{x}$+$\frac{z}{x}$+$\frac{z}{y}$+3
=$\frac{x+z}{y}$+$\frac{x+y}{z}$+$\frac{y+z}{x}$+3.
∵x+y+z=0,
∴x+z=-y,x+y=-z,y+z=-x,
∴原式=$\frac{x+z}{y}$+$\frac{x+y}{z}$+$\frac{y+z}{x}$+3
=-1-1-1+3
=0.
故选A.
点评 本题考查了分式的化简求值,解答本题的关键在于将原式化简为$\frac{x+z}{y}$+$\frac{x+y}{z}$+$\frac{y+z}{x}$+3,然后根据x+y+z=0,求出x+z=-y,x+y=-z,y+z=-x.

练习册系列答案
 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
1.平面直角坐标系内有一点A(a,b),若ab=0,则点A的位置在( )
| A. | 原点 | B. | x轴上 | C. | y轴上 | D. | 坐标轴上 |
5. 我们用如图的方法来修理一条摇晃的凳子是根据( )
我们用如图的方法来修理一条摇晃的凳子是根据( )
 我们用如图的方法来修理一条摇晃的凳子是根据( )
我们用如图的方法来修理一条摇晃的凳子是根据( )| A. | 两点之间线段最短 | B. | 矩形的对称性 | ||
| C. | 矩形的四个角都是直角 | D. | 三角形具有稳定性 |
2.下列图形是由大小相同的小黑点与大小相同的正三角形按一定规律组成的图形,第①个图形中小黑点与正三角形的个数和为4,第②个图形中小黑点与正三角形的个数和为8,第③个图形中小黑点与正三角形的个数和为13,第④个图形中小黑点与正三角形的个数和为20,…,则第8个图形中小黑点与正三角形的个数和为( )
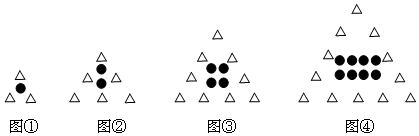

| A. | 88 | B. | 91 | C. | 152 | D. | 155 |
3.在平面直角坐标系中,点(m,n)关于原点对称的点的坐标是( )
| A. | (m,n) | B. | (-m,-n) | C. | (n,-m) | D. | (n,m) |
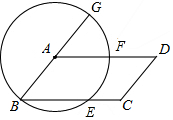 如图,以□ABCD的顶点A为圆心,AB为半径作⊙A,分别交BC,AD于E,F两点,交BA的延长线于G,判断$\widehat{EF}$和$\widehat{FG}$是否相等,并说明理由.
如图,以□ABCD的顶点A为圆心,AB为半径作⊙A,分别交BC,AD于E,F两点,交BA的延长线于G,判断$\widehat{EF}$和$\widehat{FG}$是否相等,并说明理由.