题目内容
(10分)如图,在△ABC中,AB=AC,以AB为直径的⊙O交BC于点D,过
点D作EF⊥AC于点E,交AB的延长线于点F.
(1)求证:EF是⊙O的切线;
(2)当∠BAC=60º时,DE与DF有何数量关系?请说明理由;
(3)当AB=5,BC=6时,求tan∠BAC的值.
(1) 证明:连结OD,
∵AB=AC,∴∠2=∠C
又∵OD=OB,∴∠2=∠1
∴∠1=∠C
∴OD∥AC
∵EF⊥AC
∴OD⊥EF
∴EF是⊙O的切线。
(2)DE与DF的数量关系为:DF=2DE。理由如下:
连结AD
∵AB是⊙O的直径,∴AD⊥BC,
∵AB=AC。 ∴∠3=∠4=![]() ∠BAC=30°
∠BAC=30°
∵∠F=90°-∠BAC=90°-60°=30°,∴∠3=∠F
∴AD=DF
∵∠4=30°,EF⊥AC,∴AD=2DE
∴DF=2DE.
(3)解:设⊙O与AC的交点为P,连结BP,则BP⊥AC,由上知BD=![]() BC=3
BC=3
∴![]()
![]()
∴![]()
∴![]()
∴![]()
∴tan∠BAC=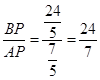
解析:略

练习册系列答案
相关题目

 中,
中,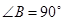 ,
,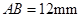 ,
,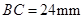 ,动点
,动点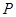 从点
从点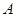 开始沿边
开始沿边 向
向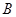 以
以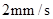 的速度移动(不与点
的速度移动(不与点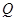 从点
从点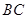 向
向 以
以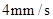 的速度移动(不与点
的速度移动(不与点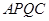 的面积最小;(2)面积最小是多少?
的面积最小;(2)面积最小是多少?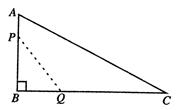
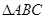 中,点
中,点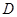 在边
在边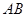 上,点
上,点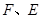 在边
在边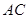 上,且
上,且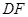 ∥
∥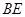 ,
,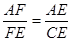 .
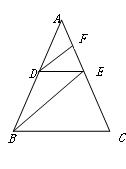
.
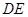 ∥
∥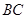 ;(5分)
;(5分)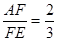 ,
,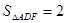
 ,求
,求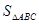 的值.(5分)
的值.(5分) =
= 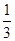 .求证:
.求证: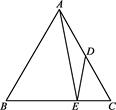
 ,求
,求