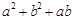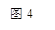题目内容
(本题10分)
如图,在正△ABC中,点D是AC的中点,点E在BC上,且 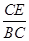 =
= 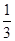 .求证:
.求证: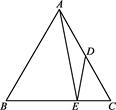
(1)△ABE∽△DCE;
(2)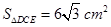 ,求
,求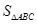
(1)∵ΔABC是正三角形
∴∠B=∠C,AB=AC
∵点D是AC的中点 ∴AC=2CD
∵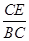 =
= 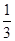 ∴BE=2CE
∴BE=2CE
∴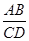 =
= 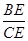 ∴ΔABE∽ΔDCE
∴ΔABE∽ΔDCE
(2)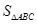 =
= 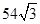
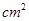
解析试题分析:证明:(1)∵ΔABC是正三角形
∴∠B=∠C,AB=AC
∵点D是AC的中点 ∴AC=2CD
∵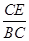 =
= 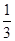
∴BE=2CE
∴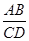 =
= 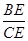 ∴ΔABE∽ΔDCE
∴ΔABE∽ΔDCE
(2)由(1)知,ΔABE∽ΔDCE,且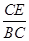 =
= 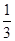 ,
, =(
=(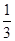 )2=
)2=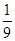 ,
,
∵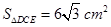
∴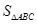 =
= 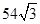
考点:相似三角形
点评:难度较低。考查相似三角形的判定与相似三角形的面积比。题(1)考查相似三角形的判定,通过证明一对对应角相等和两对对应边的比相等,证出两个三角形相似。(2)考查相似三角形的面积比等于对应 (边/高/中线/角分线)的平方比。

练习册系列答案
相关题目

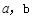 的矩形,它的周长为14,面积为10,求下列各式的值:(1)
的矩形,它的周长为14,面积为10,求下列各式的值:(1)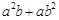 (2)
(2)