题目内容
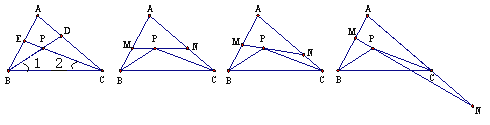
【题目】如图①,△ABC的角平分线BD、CE相交于点P.
(1)如果∠A=70°,求∠BPC的度数;
(2)如图②,过P点作直线MN∥BC,分别交AB和AC于点M和N,试求∠MPB+∠NPC的度数(用含∠A的代数式表示);
① ② ③ ④
在(2)的条件下,将直线MN绕点P旋转.
(ⅰ)当直线MN与AB、AC的交点仍分别在线段AB和AC上时,如图③,试探索∠MPB、∠NPC、∠A三者之间的数量关系,并说明你的理由;
(ⅱ)当直线MN与AB的交点仍在线段AB上,而与AC的交点在AC的延长线上时,如图④,试问(ⅰ)中∠MPB、∠NPC、∠A三者之间的数量关系是否仍然成立?若成立,请说明你的理由;若不成立,请给出∠MPB、∠NPC、∠A三者之间的数量关系,并说明你的理由.
【答案】(1)125°;(2)∠MPB+∠NPC=90°-![]() ∠A;(3)∠MPB+∠NPC= 90°-
∠A;(3)∠MPB+∠NPC= 90°-![]() ∠A,∠MPB-∠NPC=90°-
∠A,∠MPB-∠NPC=90°-![]() ∠A.
∠A.
【解析】
试题(1)由三角形内角和定理可知∠ABC+∠ACB=180°-∠A,由角平分线的性质可知及三角形内角和定理可求出∠BPC的度数;
(2)利用平行线的性质求解或先说明∠BPC=90°+![]() ∠A;
∠A;
(3)(ⅰ)先说明∠BPC=90°+![]() ∠A,则∠MPB+∠NPC=180°-∠BPC=180°-(90°+
∠A,则∠MPB+∠NPC=180°-∠BPC=180°-(90°+![]() ∠A)= 90°-
∠A)= 90°-![]() ∠A;(ⅱ)不成立,∠MPB-∠NPC=90°-
∠A;(ⅱ)不成立,∠MPB-∠NPC=90°-![]() ∠A.理由:由图可知∠MPB+∠BPC-∠NPC=180°,由(ⅰ)知:∠BPC=90°+
∠A.理由:由图可知∠MPB+∠BPC-∠NPC=180°,由(ⅰ)知:∠BPC=90°+![]() ∠A,因此∠MPB-∠NPC=180°-∠BPC=180°-(90°+
∠A,因此∠MPB-∠NPC=180°-∠BPC=180°-(90°+![]() ∠A)= 90°-
∠A)= 90°-![]() ∠A.
∠A.
试题解析::(1)∵在△ABC中,∠A+∠B+∠ACB=180°,
∵∠A=70°,
∴∠ABC+∠ACB=110°,
∵∠1=![]() ∠ABC,
∠ABC,
∠2=![]() ∠ACB,
∠ACB,
∴∠1+∠2=![]() (∠ABC+∠ACB)
(∠ABC+∠ACB)
=![]() ×110°=55°,
×110°=55°,
∴∠BPC=180°-(∠1+∠2)=180°-55°=125°;
(2)由(1)可证∠BPC=90°+![]() ∠A,
∠A,
∴∠MPB+∠NPC=180°-∠BPC=180°-(90°+![]() ∠A)=90°-
∠A)=90°-![]() ∠A;
∠A;
(3)(ⅰ)∠MPB+∠NPC= 90°-![]() ∠A.
∠A.
理由:先说明∠BPC=90°+![]() ∠A,则∠MPB+∠NPC=180°-∠BPC=180°-(90°+
∠A,则∠MPB+∠NPC=180°-∠BPC=180°-(90°+![]() ∠A)= 90°-
∠A)= 90°-![]() ∠A;
∠A;
(ⅱ)不成立(1分),∠MPB-∠NPC=90°-![]() ∠A(1分).
∠A(1分).
理由:由图可知∠MPB+∠BPC-∠NPC=180°,由(ⅰ)知:∠BPC=90°+![]() ∠A,
∠A,
∴∠MPB-∠NPC=180°-∠BPC=180°-(90°+![]() ∠A)= 90°-
∠A)= 90°-![]() ∠A.
∠A.
考点: (1)平行线的性质;2.角平分线的性质;3.三角形内角和.

 智能训练练测考系列答案
智能训练练测考系列答案【题目】超越公司将某品牌农副产品运往新时代市场进行销售,记汽车行驶时为t小时,平均速度为v千米/小时(汽车行驶速度不超过100千米/小时).根据经验,v,t的一组对应值如下表:
v(千米/小时) | 75 | 80 | 85 | 90 | 95 |
t(小时) | 4.00 | 3.75 | 3.53 | 3.33 | 3.16 |
(1)根据表中的数据,求出平均速度v(千米/小时)关于行驶时间t(小时)的函数表达式;
(2)汽车上午7:30从超越公司出发,能否在上午10:00之前到达新时代市场?请说明理由.