题目内容
已知抛物线①经过点A（-1,0）、B（4,5）、C（0,-3），其对称轴与直线BC交于点P。
（1）求抛物线①的表达式及点P的坐标；
（2）将抛物线①向右平移1个单位后再作上下平移，得到的抛物线②恰好过点P，求上下平移的方向和距离；
（3）设抛物线②的顶点为D，与y轴的交点为E，试求∠EDP的正弦值。
解：（1）据题意设抛物线的表达式为
，
则
，解得
，∴抛物线的表达式为
∴对称轴为直线
据题意设直线BC的解析式为
，则
，
∴直线BC的解析式为
，∴P（1，-1）
（2）设抛物线①向右平移1个单位后再向上平移m个单位得抛物线②，
则抛物线②的表达式为
∵抛物线②过点P，∴
，∴
∴再将它向上移动2个单位可得到抛物线②
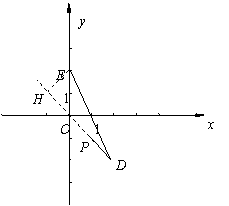
（3）∵抛物线①向右移动1个单位，再向上平移2个单位得到抛物线②，
∴抛物线②的表达式是
即
，∴D（2,-2），E（0,2）
∵P(1,-1)，∴直线DP过点O，且与x轴夹角为45°，
过点E作EH⊥DP于点H，∴∠EOH= 45°
∵E（0,2）,∴EH=
，而ED=
∴sin∠EDP=
练习册系列答案
相关题目
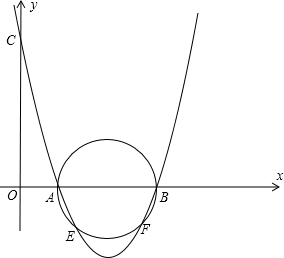已知抛物线经过点A（1，0）、B（3，0）、C（0，3），以AB为直径画圆．
如图，已知抛物线经过点A（-3，0），B（0，3），C（2，0）三点．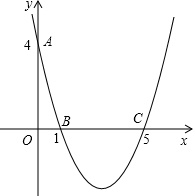
如图，在平面直角坐标系xoy中，已知抛物线经过点A（0，4），B（1，0），C（5，0），抛物线对称轴l与x轴相交于点M．