题目内容
 如图,一次函数y=-
如图,一次函数y=- x-2的图象分别交x轴、y轴于点A、B,点P为AB延长线上一点,且
x-2的图象分别交x轴、y轴于点A、B,点P为AB延长线上一点,且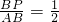 ,过P作y轴的平行线分别交x轴于C,交反比例函数
,过P作y轴的平行线分别交x轴于C,交反比例函数 (k>0)的图象于点Q,四边形OBPQ的面积为8.
(k>0)的图象于点Q,四边形OBPQ的面积为8.
(1)求A、B两点的坐标及k的值;
(2)求线段OQ所在直线的函数关系式.
解:(1)∵一次函数y=- x-2的图象分别交x轴、y轴于点A、B,
x-2的图象分别交x轴、y轴于点A、B,
∴A(-4,0),B(0,-2).
∵PQ∥OB,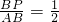 ,
,
又∵S△ABO=4,
∴S△APC=9,
∴S四边形OBPC=5,
∵四边形OBPQ的面积为8,
∴S△QCO=3,
∵k>0,
∴k=6;
(2)设线段OQ所在直线的解析式为y=kx,
∵OC=2,即xQ=2,代入y=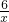 ,得yQ=3,
,得yQ=3,
∴Q(2,3)
∴线段OQ所在直线的函数关系式为y=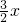 .
.
分析:(1)分别令x=0和y=0解得y和x的值分别是A点的横坐标和B点的纵坐标;
(2)求得Q点的坐标代入正比例函数的解析式即可求得其解析式.
点评:本题考查了待定系数法求反比例函数解析式以及待定系数法求一次函数解析式,利用图象判定函数的大小关系是中学的难点,同学们应重点掌握.
 x-2的图象分别交x轴、y轴于点A、B,
x-2的图象分别交x轴、y轴于点A、B,∴A(-4,0),B(0,-2).
∵PQ∥OB,
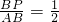 ,
,又∵S△ABO=4,
∴S△APC=9,
∴S四边形OBPC=5,
∵四边形OBPQ的面积为8,
∴S△QCO=3,
∵k>0,
∴k=6;
(2)设线段OQ所在直线的解析式为y=kx,
∵OC=2,即xQ=2,代入y=
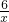 ,得yQ=3,
,得yQ=3,∴Q(2,3)
∴线段OQ所在直线的函数关系式为y=
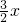 .
.分析:(1)分别令x=0和y=0解得y和x的值分别是A点的横坐标和B点的纵坐标;
(2)求得Q点的坐标代入正比例函数的解析式即可求得其解析式.
点评:本题考查了待定系数法求反比例函数解析式以及待定系数法求一次函数解析式,利用图象判定函数的大小关系是中学的难点,同学们应重点掌握.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
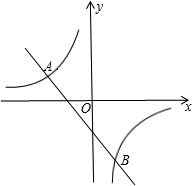 已知,如图,一次函数y1=-x-1与反比例函数y2=-
已知,如图,一次函数y1=-x-1与反比例函数y2=-| 2 |
| x |
| A、x>1 |
| B、x<-2或0<x<1 |
| C、-2<x<1 |
| D、-2<x<0或x>1 |
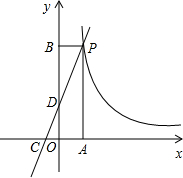 如图,一次函数y=kx+2的图象与反比例函数y=
如图,一次函数y=kx+2的图象与反比例函数y=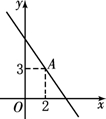 13、如图,一次函数y=kx+b(k<0)的图象经过点A.当y<3时,x的取值范围是
13、如图,一次函数y=kx+b(k<0)的图象经过点A.当y<3时,x的取值范围是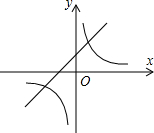 (2013•成都)如图,一次函数y1=x+1的图象与反比例函数
(2013•成都)如图,一次函数y1=x+1的图象与反比例函数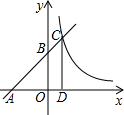 如图,一次函数y=x+3的图象与x轴、y轴分别交于点A、点B,与反比例函数
如图,一次函数y=x+3的图象与x轴、y轴分别交于点A、点B,与反比例函数