题目内容
 (2012•本溪)如图,△ABC是学生小金家附近的一块三角形绿化区的示意图,为增强体质,他每天早晨都沿着绿化区周边小路AB、BC、CA跑步(小路的宽度不计).观测得点B在点A的南偏东30°方向上,点C在点A的南偏东60°的方向上,点B在点C的北偏西75°方向上,AC间距离为400米.问小金沿三角形绿化区的周边小路跑一圈共跑了多少米?
(2012•本溪)如图,△ABC是学生小金家附近的一块三角形绿化区的示意图,为增强体质,他每天早晨都沿着绿化区周边小路AB、BC、CA跑步(小路的宽度不计).观测得点B在点A的南偏东30°方向上,点C在点A的南偏东60°的方向上,点B在点C的北偏西75°方向上,AC间距离为400米.问小金沿三角形绿化区的周边小路跑一圈共跑了多少米?(参考数据:
| 2 |
| 3 |
分析:延长AB至D点,作CD⊥AD于D,根据题意得∠BAC=30°,∠BCA=15°,利用三角形的外角的性质得到∠DBC=∠DCB=45°,然后在Rt△ADC中,求得CD=BD=200米后即可求得三角形ABC的周长.
解答: 解:过点C作CD⊥AB交AB延长线于一点D,
解:过点C作CD⊥AB交AB延长线于一点D,
根据题意得∠BAC=30°,∠BCA=15°,
故∠DBC=∠DCB=45°,
在Rt△ADC中,
∵AC=400米,∠BAC=30°,
∴CD=BD=200米,
∴BC=200
米,AD=200
米
∴AB=AD-BD=(200
-200)米,
∴三角形ABC的周长为400+200
+(200
-200)≈829米
小金沿三角形绿化区的周边小路跑一圈共跑了约829米.
 解:过点C作CD⊥AB交AB延长线于一点D,
解:过点C作CD⊥AB交AB延长线于一点D,根据题意得∠BAC=30°,∠BCA=15°,
故∠DBC=∠DCB=45°,
在Rt△ADC中,
∵AC=400米,∠BAC=30°,
∴CD=BD=200米,
∴BC=200
| 2 |
| 3 |
∴AB=AD-BD=(200
| 3 |
∴三角形ABC的周长为400+200
| 2 |
| 3 |
小金沿三角形绿化区的周边小路跑一圈共跑了约829米.
点评:本题考查了解直角三角形的应用,解题的关键是从实际问题中整理出直角三角形模型并求解.

练习册系列答案
相关题目
 (2012•本溪)如图所示的几何体的俯视图是( )
(2012•本溪)如图所示的几何体的俯视图是( )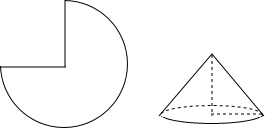 (2012•本溪)如图,用半径为4cm,弧长为6πcm的扇形围成一个圆锥的侧面,则所得圆锥的高为
(2012•本溪)如图,用半径为4cm,弧长为6πcm的扇形围成一个圆锥的侧面,则所得圆锥的高为 (2012•本溪)如图,矩形ABCD中,点P、Q分别是边AD和BC的中点,沿过C点的直线折叠矩形ABCD使点B落在线段PQ上的点F处,折痕交AB边于点E,交线段PQ于点G,若BC长为3,则线段FG的长为
(2012•本溪)如图,矩形ABCD中,点P、Q分别是边AD和BC的中点,沿过C点的直线折叠矩形ABCD使点B落在线段PQ上的点F处,折痕交AB边于点E,交线段PQ于点G,若BC长为3,则线段FG的长为