题目内容
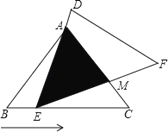
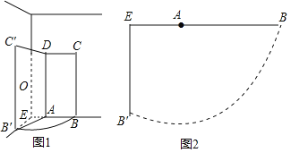
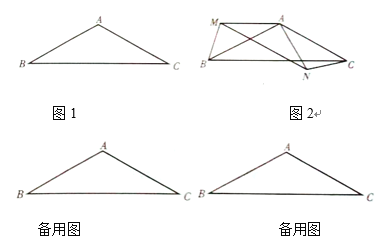
【题目】如图1,在![]() 中,
中,![]() ,
,![]() .
.
问题情境1:(1)![]() 与
与![]() 的数量关系为_______;
的数量关系为_______;
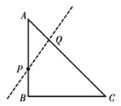
问题情境2:(2)如图2,若![]() ,且
,且![]() ,则
,则![]() 与
与![]() 的数量关系是什么.请说明理由;
的数量关系是什么.请说明理由;
拓展延伸:(3)将图2中的![]() 绕点
绕点![]() 顺时针旋转角度
顺时针旋转角度![]() (
(![]() ),在旋转过程中,当
),在旋转过程中,当![]() ,
,![]() ,
,![]() 三点在同一条直线上时,请直接写出
三点在同一条直线上时,请直接写出![]() ,
,![]() ,
,![]() 之间的数量关系.
之间的数量关系.
【答案】(1)![]() ;(2)
;(2)![]() ,理由见解析;(3)
,理由见解析;(3)![]() 或
或![]() .
.
【解析】
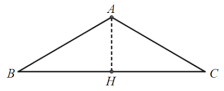
(1)如图,作AH⊥BC于H.解直角三角形即可解决问题;
(2)证明△AMB≌△ANC即可得到BM=CN;
(3)如图3中,作AH⊥MN于H.由△MAB≌△NAC,推出BM=CN,在Rt△AMH中,MH=AMcos30°=![]() AM,由AM=AN,AH⊥MN,推出MH=HN,可得CM=MN+NC=2MH+BM=
AM,由AM=AN,AH⊥MN,推出MH=HN,可得CM=MN+NC=2MH+BM=![]() AM+BM;如图4中,同理可得:BM=CM+
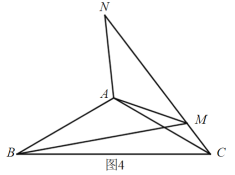
AM+BM;如图4中,同理可得:BM=CM+![]() AM.
AM.
解:(1)![]() ,
,
如图,作AH⊥BC于H.
∵AB=AC,AH⊥BC,
∴BH=HC,
∵∠BAC=120°,
∴∠B=∠C=30°,
在Rt△ABH中,cos∠ABH=![]() ,
,
∴BH=AB∠ABH=ABcos30°=![]()
∴BC=2BH=![]() .
.
(2)![]() .
.
理由如下:
![]() ,
,
![]() ,
,![]() .
.
![]() ,
,
![]() ,
,
![]() ,
,
即![]() .
.
在![]() 和
和![]() 中,
中,
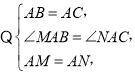
![]() ,
,
![]()
(3)如图3中,作AH⊥MN于H.
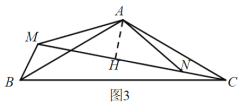
∵△MAB≌△NAC,
∴BM=CN,
在Rt△AMH中,MH=AMcos30°=![]() AM,
AM,
∵AM=AN,AH⊥MN,
∴MH=HN,
∵CM=MN+CN=2MH+BM=![]() AM+BM.
AM+BM.
如图4中:C,M,N共线时,同理可得:BM=CM+![]() AM.
AM.
∴![]() 或
或![]() .
.

练习册系列答案
相关题目